本解法比较适合小白 （图解+详细分析+朴素解法）

算法思路：贪心、转化

1、题目给了我们很多个点，以及单个雷达扫描的范围，想让我们求一下在 $x$ 轴上至少需要多少个雷达能把所有个点全部覆盖住

2、其实很多问题都和这题思维方式很相似，如果我们直接去考虑一个问题发现不那么容易考虑的时候，我们可以想办法把它做一个转化，转化成我们容易考虑的形式

3、就这个题目而言，我们如果直接去考虑的话，是需要处理很多的圆，因为雷达扫描是以圆为范围进行覆盖的，所以我们需要考虑要多数个圆才能把所有的点覆盖住

4、可是圆的特殊性导致我们无法很好的用一个规律去总结出最优解，我也尝试过正面去做，发现确实很难，所以我们需要转化

5、如何转化呢？我们一开始是以雷达的角度去思考这个问题，但是我们完全可以换一个思考对象，那就是对于点来分析

6、既然是对于点来分析，那么该如何操作呢？

7、我们可以这么考虑，雷达扫描的范围，也就是半径是已知的，并且雷达也就是圆心一定在 $x$ 轴上，所以我们可以根据这个信息，对于每个点来说，都能计算出能够覆盖该点的，雷达位置的取值范围，也就是圆心的取值范围

8、怎么计算呢？我们假设能覆盖到该点的雷达的坐标为 ($x$,0)，而该点的坐标为 ($x_1$,$y_1$),那么我们就可以得到，能够覆盖该点的 $x$ 的取值范围(计算边界即可)，下面进行公式的推导

9、那么根据上图我们就求出了 每个点，对应的，能够扫描到它的，雷达的范围，即求出来的 $l$ 到 $r$ ，就是在 $x$ 轴上的可以扫描到该点的范围

10、那么我们对于每个点都可以求出，在 $x$ 轴上的一个范围，使得在这个范围内的雷达都能够扫描到该点

11、我们计算出了这个有什么用呢？

12、通过计算这个区间我们就把原来的 “由雷达去扫描点” 的问题转化成了 “用点来确定雷达位置” 的问题

13、那么我们计算出的区间有什么用呢？

14、我们随机拿出两个点，它们都有对应的区间，那么它们的区间关系无非以下两种情况

15、通过图中的分析可以知道，任意两个点的区间关系无非两种，要么存在交集，要么不存在交集。其中，如果两个点存在交集，那么这两个点只需要一个雷达既可以覆盖；如果不存在交集，那么则需要两个雷达进行覆盖

16、那么加上这个信息，我们就可以知道，要计算至少要多少个雷达能够覆盖所有的点，也就是考虑一下每个点对应的区间的关系就可以了，只要把区间的关系搞清楚了，那么需要多少个雷达也就解决了。

17、既然我们要弄清楚各个点对应的区间的关系的话，那我们就需要弄清楚任意两个点之间的区间关系。

18、如果我们对于某个点都去遍历一边其他点的话，未免过于复杂，所以我们需要优化

19、不难想到，既然我们要求区间之间的关系，而且这种关系是和顺序没有关系的，所以我们可以考虑把区间排序。这其实也是一种思想，把无序的转化成有序的往往更容易操作

20、那么这里又有一个问题了，那我们是以区间的左端点作为区间的排序依据（即按左端点大小来排序），还是以右端点来排序呢（即按右端点的大小来排序）？

21、这边我先告诉大家结论，晚点会证明为什么需要这样。结论就是我们需要按照区间的右端点进行排序（稍后会解释）

22、那我们对于好序后的区间应该如何操作呢？假设我们现在有 $n$ 个点，那么对应的就会有 $n$ 个区间，那么我们如何求呢？

23、从上图可以看到，我们以第一个区间的右端点为起点，从前往后遍历所有的区间，里面谈到了一个动态维护区间的概念，那么我们应该如何具体实现呢？

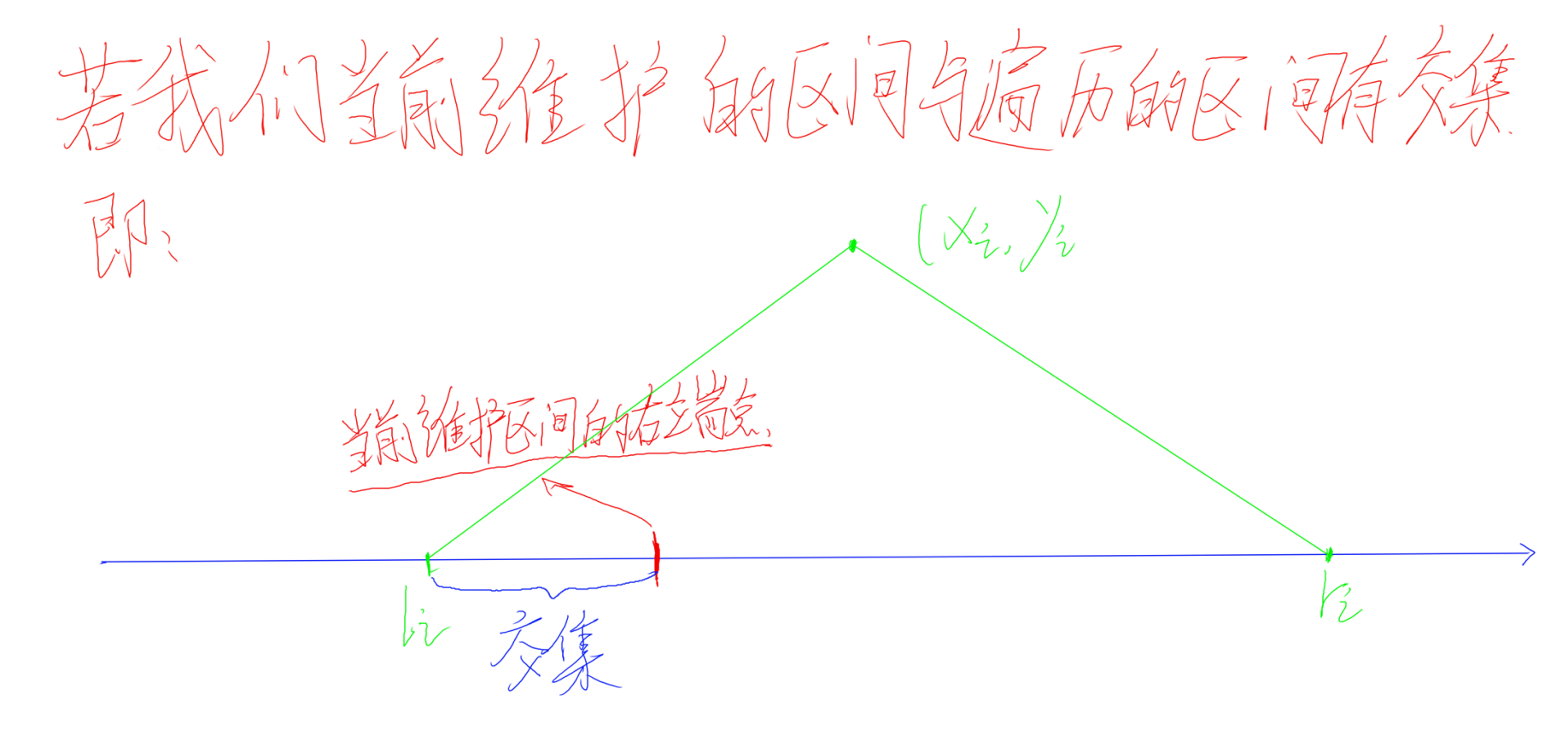
(先解释一下，我们当前维护的区间的本质是当前雷达能够安装的范围)

24、如果是上图的情况，我们当前维护的区间，与遍历到的区间有交集的话，那么说明我们当前的雷达能够覆盖该点（因为在我们当前雷达能够安装的范围内能够扫描到该点），那么我们就跳过这个点（因为不需要多增添雷达），再遍历后面的点

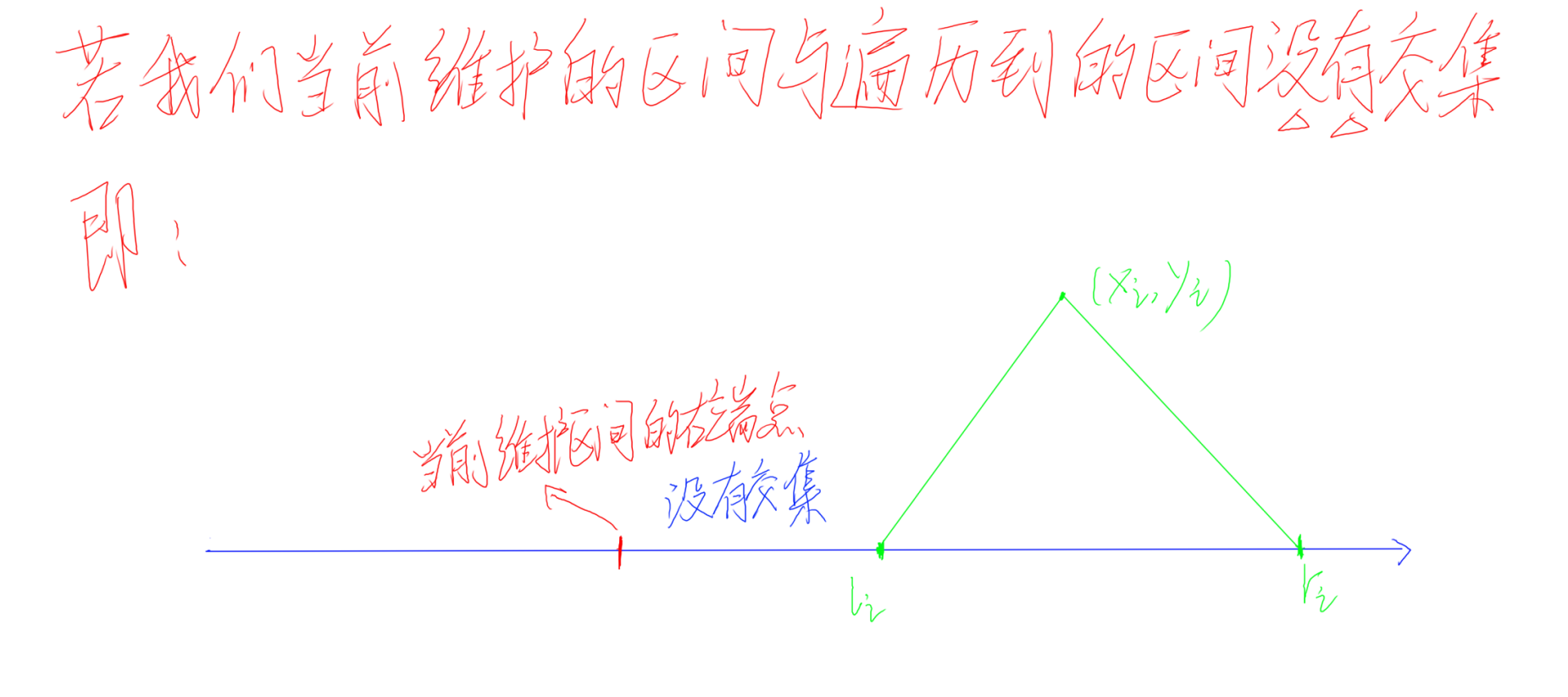
25、如果是上图的情况，我们当前维护的区间，与遍历到的区间没有交集的话，那么说明我们当前的雷达无法覆盖该点（因为在我们当前雷达能够安装的范围无法扫描到该点），所以我们就要增加一个雷达，用来扫描该点。而与此同时，我们就要把我们当前维护的区间的右端点，修改为这个遍历到的区间的右端点（为什么要修改呢？因为我们增添了一个新的雷达，那么我们雷达能够安装的范围就变了，所以我们要更新一下我们维护的区间）

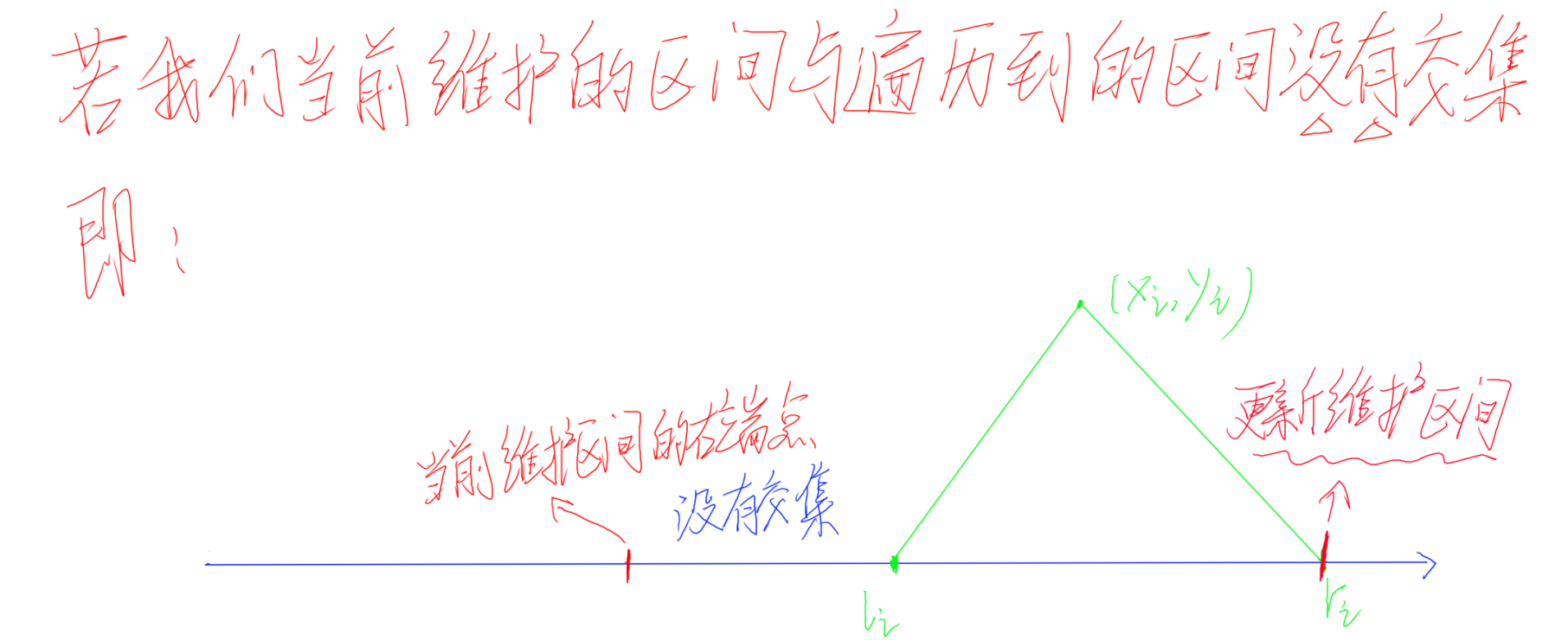
26、用上述方法，把排好序后的区间，从 1 到 $n$ 依次按照上述操作遍历，就可以求出我们所需要的雷达数量

27、最后我们来解释一下前面提到的，为什么要把各个区间以右端点为标准进行排序？请看下面这张图

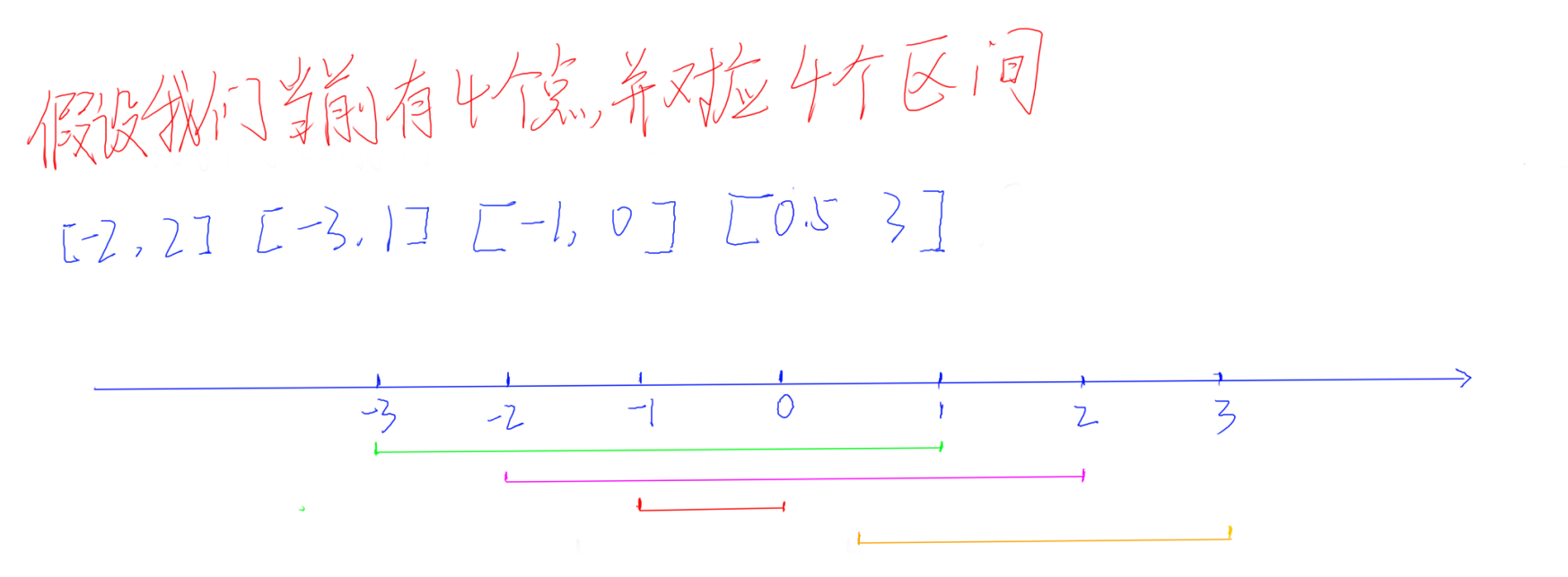
28、上图中表示了 4 个点以及其对应的区间，现在我们以左端点为排序标准，我们用我们上述的方法进行判断，我们以第一个区间（也就是区间[-3,1]）的右端点为当前维护区间的端点，往后遍历。会发现，后面的每一个区间的左端点都小于我们的当前维护区间的端点，根据上述方法，那么我们只需要一个雷达就可以覆盖这 4 个点。

29、但事实并非如此。现在我们以右端点为排序标准，我们再用上述方法进行判断，那我们的第一个区间就变成了 [-1,0]，那么我们当前维护区间的右端点就是 0 ，然后往后遍历。可以发现，当遍历到最后一个区间 [0.5,3]的时候，这个区间的左端点就大于我们当前维护的区间的端点 0（前面的两个区间的左端点都是小于 0 的 ） ，那么根据我们上述的方法，我们就需要多加一个雷达，所以此时我们需要两个雷达才可以覆盖所有的点。

30、所以，如果以左端点为排序标准，很可能会出现错误，正解应该是以右端点为排序标准。

31、写这篇题解时间跨度有点长，花了我三天的时间，因为平时也比较忙。所以这篇题解可能有些地方讲的不是很清楚的，不懂的同学可以在评论区告诉我，我再来更正！

#include<iostream>
#include<cstring>
#include<algorithm>
#include<cstdio>
#include<cmath>

//动态的维护雷达所能扫描到的范围

#define l first// l 表示左边界

#define r second// r 表示右边界

using namespace std;

typedef long long LL;

const int N=1010;

int n;

typedef pair<double,double>PII;

PII a[N];//LL
PII c[N];//LL

LL d;

bool cmp(PII A,PII B)//比较函数，让pair<double,double>类型的数组以后面的大小为依据来排序
{
    return A.r<B.r;
}
int main()
{
    scanf("%d%lld",&n,&d);

    for(int i=1;i<=n;i++)scanf("%lf%lf",&a[i].l,&a[i].r);//读入每个点


    bool flag=true;//用于判断是否有点无法覆盖到


    for(int i=1;i<=n;i++)//计算出我们每个点对应的雷达  可以安放的范围  也就是把我们的点转化成了范围
    {
        if(4*a[i].l*a[i].l+4*(d*d-a[i].l*a[i].l-a[i].r*a[i].r)>=0)//判断是否有解
        {
            c[i].l=a[i].l-(sqrt(4*a[i].l*a[i].l+4*(d*d-a[i].l*a[i].l-a[i].r*a[i].r)))/2;//数学公式推导出来的，左端点

            c[i].r=a[i].l+(sqrt(4*a[i].l*a[i].l+4*(d*d-a[i].l*a[i].l-a[i].r*a[i].r)))/2;//右端点
        }
        else//如果误解说明覆盖不到，那就false，直接退出
        {
            flag=false;

            break;
        }
    }

    sort(c+1,c+n+1,cmp);//这边要根据区间的右端点进行排序，如果不按照这个规则进行排序会出错

    double weizhi=c[1].r;//把第一个点的右端点记为起始位置，然后动态的维护一下我们当前雷达所能扫描的范围

     int ans=1;//答案初始化为 1 ，因为我们一开始就放了一个雷达用于满足第一个点（因为我们把第一个点的右端点作为了起始位置）

    for(int i=1;i<=n;i++)
    {

        if(c[i].l>weizhi)
       //如果我们当前的点 所需要的雷达的区间的左端点大于我们目前的位置，那么说明我们此时雷达的覆盖范围不够了，所以要新增一个雷达
        {
            ans++;

            weizhi=c[i].r;//更新一下我们雷达所能扫描的范围
        }

    }

    if(flag)//如果我们所有的点都能被覆盖到，就输出结果
   printf("%d",ans);

   else//如果存在点不能被覆盖到，那就输出 -1
   printf("-1");

    return 0;
}

画图码字不易，点个赞再走呗~