题目描述

给你两个单词 word1 和 word2，请你计算出将 word1 转换成 word2 所使用的最少操作数 。

你可以对一个单词进行如下三种操作：

插入一个字符
删除一个字符
替换一个字符

示例 1：

输入：word1 = “horse”, word2 = “ros”
输出：3
解释：
horse -> rorse (将 ‘h’ 替换为 ‘r’)
rorse -> rose (删除 ‘r’)
rose -> ros (删除 ‘e’)
示例 2：

输入：word1 = “intention”, word2 = “execution”
输出：5
解释：
intention -> inention (删除 ‘t’)
inention -> enention (将 ‘i’ 替换为 ‘e’)
enention -> exention (将 ‘n’ 替换为 ‘x’)
exention -> exection (将 ‘n’ 替换为 ‘c’)
exection -> execution (插入 ‘u’)

提示：

0 <= word1.length, word2.length <= 500
word1 和 word2 由小写英文字母组成

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/edit-distance
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

算法1

(DP) $O(n^2)$

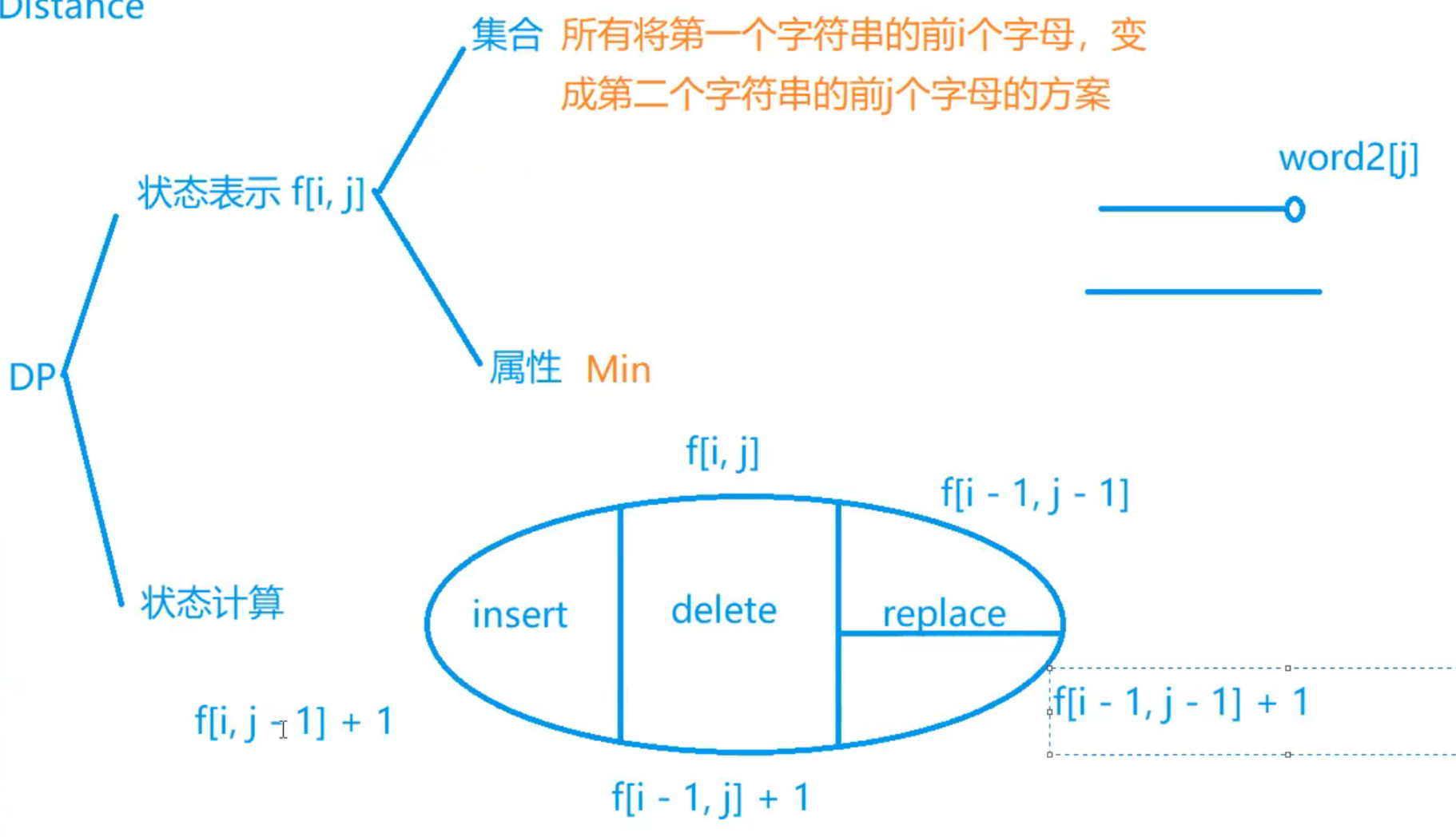
插入：
ros i = 2
rose j = 3 单词1的前i个字母与单词2前j-1个字母匹配 f[i,j-1] + 1;
删除：
rose i = 1
rse j = 0 单词1的前i-1个字母与单词2前j个字母匹配 f[i-1,j] + 1;
替换：
（1）
rose i = 3
rose j = 3 单词1的第i个字母与单词2第j个字母匹配 f[i-1,j-1]
（2）
rosa i = 3
rose j = 3 单词1的第i个字母与单词2第j个字母不匹配 f[i-1,j-1] + 1 （操作步骤数）

时间复杂度

参考文献

C++ 代码

class Solution {
public:
    int minDistance(string word1, string word2) {
        int n = word1.size(), m = word2.size();
        vector<vector<int>> f(n+1,vector<int>(m+1));
        for(int i=0; i<=n; ++i) f[i][0] = i;   //将world1的前i个字符，变为world2 的前0个字符；执行删除
        for(int i=0; i<=m; ++i) f[0][i] = i;   //将world1的前0个字符，变为world2 的前i个字符；执行插入

        for(int i=1; i<=n; ++i){
            for(int j=1; j<=m; ++j){
                f[i][j] = min(f[i][j-1], f[i-1][j]) + 1;    //插入：前i个字母与前j-1个字母匹配  f[i][j-1] +1
                                                            //或者 删除：前i-1个字母与前j个字母匹配 f[i-1][j]+1

                if(word1[i-1] != word2[j-1])  f[i][j] = min(f[i][j], f[i-1][j-1] + 1);  //如果word1 与 word2的字符 i== j，则不用替换，直接找到最小值
                else  f[i][j] = min(f[i][j], f[i-1][j-1]);  //否则替换执行操作
            }
        }
        return f[n][m];  //word 从 1 开始计数
    }
};