题目描述

blablabla

给你一个整数数组 nums ，找到其中最长严格递增子序列的长度。

子序列是由数组派生而来的序列，删除（或不删除）数组中的元素而不改变其余元素的顺序。例如，[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列。

示例 1：

输入：nums = [10,9,2,5,3,7,101,18]
输出：4
解释：最长递增子序列是 [2,3,7,101]，因此长度为 4 。
示例 2：

输入：nums = [0,1,0,3,2,3]
输出：4
示例 3：

输入：nums = [7,7,7,7,7,7,7]
输出：1

提示：

1 <= nums.length <= 2500
-104 <= nums[i] <= 104

进阶：

你可以设计时间复杂度为 O(n2) 的解决方案吗？
你能将算法的时间复杂度降低到 O(n log(n)) 吗?

算法1

(动态规划) $O(n^2)$

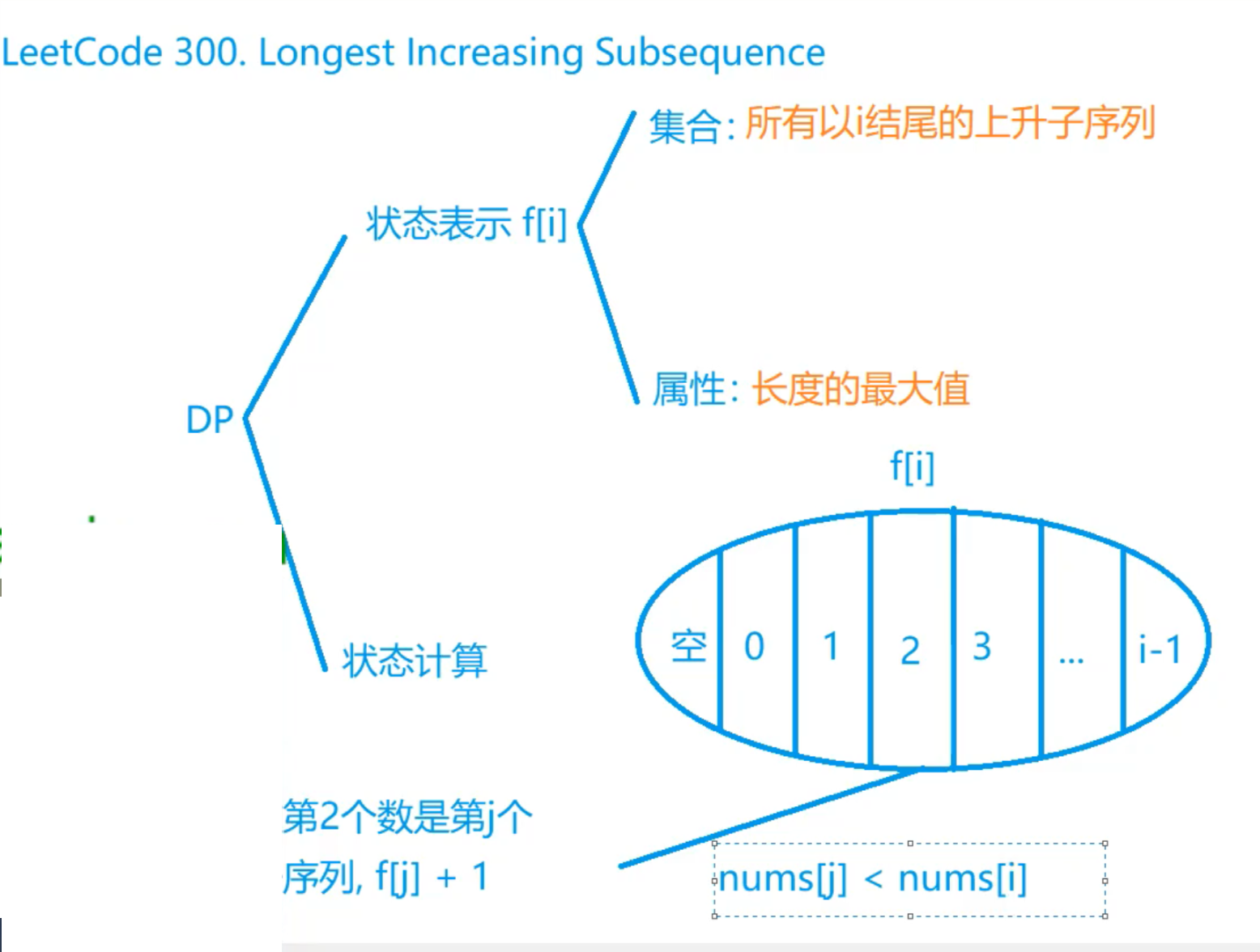
f[i]是所有以i结尾的上升子序列的集合。f[i]有很多，需要找到其中长度最大的序列。
将f[i]划分为i个子集合。f[j]表示以j结尾的上升子序列的最大值,j[HTML_REMOVED] nums[j]时成立。

遍历一遍数组 n； 每个f[i]再遍历一遍 为n，总$o(n^2)$

C++ 代码

class Solution {
public:
    int lengthOfLIS(vector<int>& nums) {
        int n = nums.size();
        vector<int> f(n);
        for(int i=0; i<n; ++i){
            f[i] = 1;
            for(int j=0; j<i; ++j){
                if(nums[i] > nums[j]){
                    f[i] = max(f[i], f[j]+1);
                }
            }
        }
        int res = 0;
        for(int i=0; i<n; ++i){
            res = max(res, f[i]);
        }
        return res;
    }
};