题目

题面

这道题的题义是说，输入一个长度为 $n$ 的序列 $A$，且有 $q$ 次操作、询问，对于其中的询问，要求给出正确答案。

操作表示为：

• 0 x y $($操作编号为 $0$，表示将 $A_x$ 修改为 $y)$。

询问表示为：

• 1 l r $($操作编号为 $1$，表示询问 $A$ 数组中 $A[l,r]$ 这个区间中的最大连续子段和$)$。

数据范围：$N,M≤5 * 10^4,|A_i|\le10^4$

解法

拿到这题后，第一想法是树状数组或线段树，因为支持修改和动态询问的比较常用的数据结构就是这两个。但是树状数组只适合求没有特殊要求的区间和，不适用于这道题目，所以就只剩下线段树了。

用线段树就要设定节点 $Node$ 里包括哪些内容。

• 区间左端点。
• 区间右端点。
• 区间最大连续子段和。

但是只知道这些信息没有办法从左右子节点得出父节点的值，我们来画图分析一下。
)
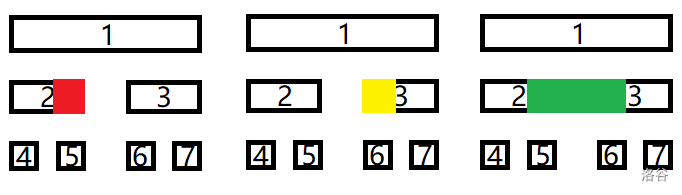
如图，$1$ 号节点的范围是 $[1,4]$，该节点的最大连续子段和所对应的区间可能是红色部分、黄色部分或绿色部分三种情况，我们来分情况讨论。

• 红色部分：可以表示为 $1$ 号节点的左儿子的最大后缀和。

• 黄色部分：可以表示为 $1$ 号节点的右儿子的最大前缀和。

• 绿色部分：可以表示为 $1$ 号节点的左儿子的最大后缀和 $+$ 右儿子的最大前缀和。

在其中取 $Max$ 即为 $1$ 号节点节点的最大连续子段和。

所以说，线段树节点中还需要包括：

• 当前区间的最大前缀和。
• 当前区间的最大后缀和。

我们再来画图考虑，如何维护一个区间的最大前后缀和。

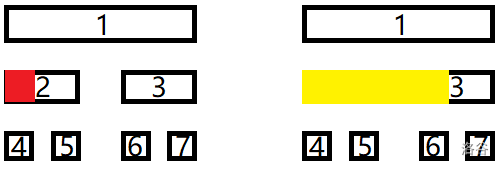
如图，$1$ 号节点的最大前缀和对应的区间有红色部分、黄色部分两种情况，分情况考虑。

• 红色部分：可以表示为 $1$ 号节点的左儿子的最大前缀和。

• 黄色部分：可以表示为 $1$ 号节点的左儿子的区间和 $+$ 右儿子的最大前缀和。

最大后缀和同理可推出两种情况。

• $1$ 号节点的右儿子的最大后缀和。

• $1$ 号节点的右儿子的区间和 $+$ 左儿子的最大后缀和。

也就是说，线段树节点中还要包含：

• 当前区间的区间和。

而当前区间的区间和就等于左儿子和右儿子的区间和之和。

总结一下，线段树的节点里就需要包括：

• 区间左端点。
• 区间右端点。
• 区间最大连续子段和。
• 当前区间的最大前缀和。
• 当前区间的最大后缀和。
• 当前区间的区间和。

再把刚才列出的计算方法套进线段树板子里就好了。

代码

代码里有注释

#include <iostream>

using namespace std;

struct Node {
  int l;     //左端点
  int r;     //右端点
  int num;   //最大连续子段和
  int lMax;  //最大前缀和
  int rMax;  //最大后缀和
  int sum;   //区间和
};

int N;
int M;
int A[50009];
Node tr[200009];

void Update (Node &f, Node left, Node right) {  //通过左右子节点更新父节点
  f.num = max(max(left.num, right.num), left.rMax + right.lMax);
  f.lMax = max(left.lMax, left.sum + right.lMax);
  f.rMax = max(right.rMax, right.sum + left.rMax);
  f.sum = left.sum + right.sum;
}

void Build (int id, int l, int r) {  //建立线段树
  int mid;

  tr[id].l = l;
  tr[id].r = r;

  if (l == r) {  //叶节点
    tr[id].num = tr[id].lMax = tr[id].rMax = tr[id].sum = A[l];
    return;
  }

  mid = (l + r) >> 1;
  Build(id * 2, l, mid);
  Build(id * 2 + 1, mid + 1, r);
  Update(tr[id], tr[id * 2], tr[id * 2 + 1]);
}

Node Query (int id, int l, int r) {  //查询区间最大连续子段和
  Node ans;
  int mid = (tr[id].l + tr[id].r) >> 1;

  if (tr[id].l > l - 1 && tr[id].r < r + 1) {  //完全包含
    return tr[id];
  }

  if (r < mid + 1) {
    return Query(id * 2, l, r);
  }
  if (l > mid) {
    return Query(id * 2 + 1, l, r);
  }

  Update(ans, Query(id * 2, l, r), Query(id * 2 + 1, l, r));  
  return ans;
}

void Change (int id, int x, int y) {  //单点修改
  int mid;

  if (tr[id].l == tr[id].r) {  //找到了区间为 [x, x] 的节点
    tr[id].num = tr[id].lMax = tr[id].rMax = tr[id].sum = y;  //修改
    return;
  }

  mid = (tr[id].l + tr[id].r) >> 1;

  if (x < mid + 1) {
    Change(id * 2, x, y);
  }
  else {
    Change(id * 2 + 1, x, y);
  }

  Update(tr[id], tr[id * 2], tr[id * 2 + 1]);  //更新
}

void In_Solve_Out () {
  int k;
  int x;
  int y;

  cin >> N;

  for (int i = 1; i < N + 1; i++) {
    cin >> A[i];
  }

  Build(1, 1, N);
  cin >> M;

  for (int m = 0; m < M; m++) {
    cin >> k >> x >> y;

    if (k == 1) {
      cout << Query(1, x, y).num << endl;
      continue;
    }

    Change(1, x, y);
  }
}

int main () {

  In_Solve_Out();

  return 0;
}