特殊情况
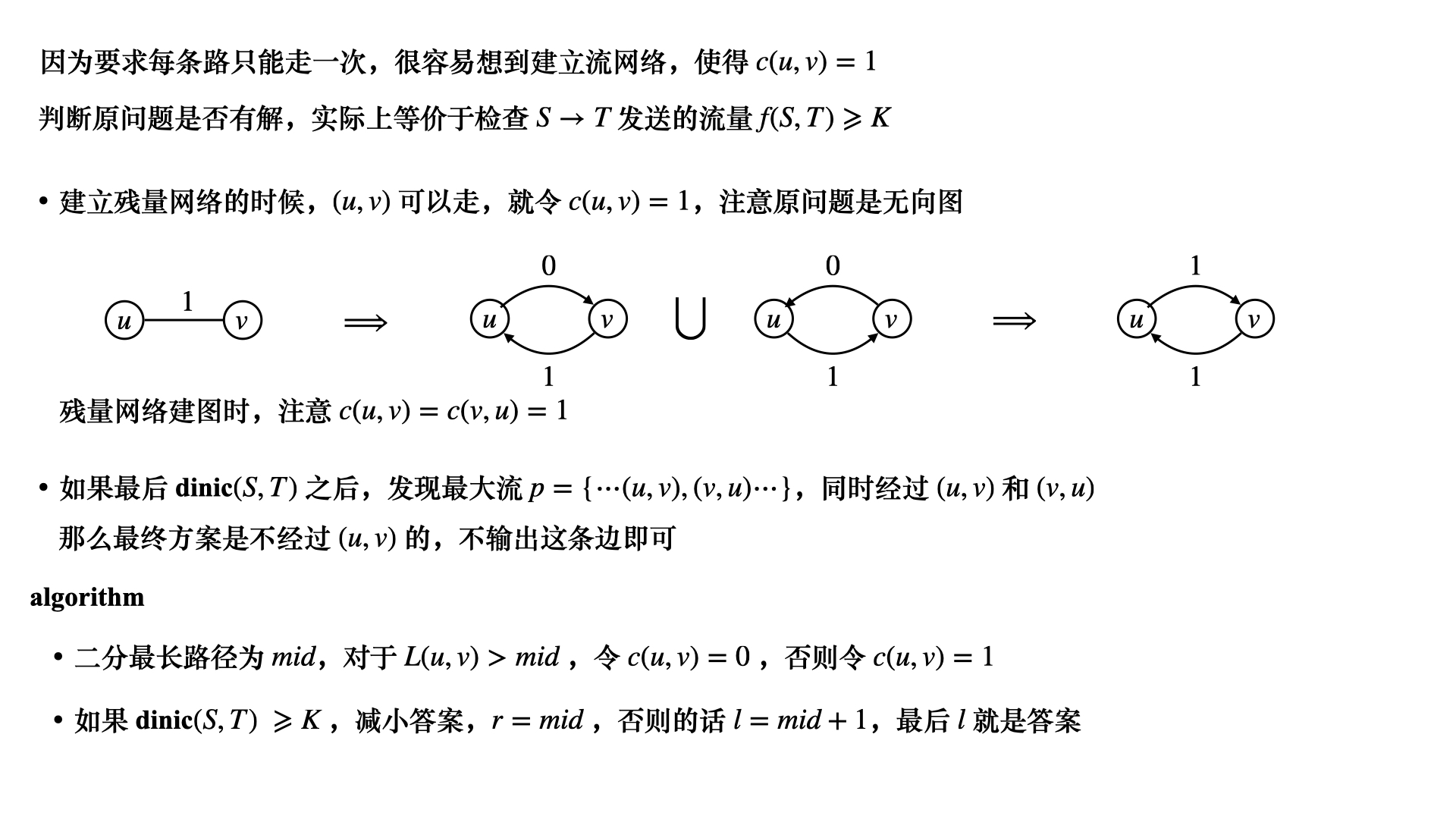
如果是无向图，要求每条边最多只能走一次，在建流网络的时候
$(u, v)$ 正向走一次，$(v, u)$ 反向又走了一次，等价于没有流
把相应的边删去即可

#include <iostream>
#include <cstdio>
#include <cstring>
#include <cstdlib>
#include <algorithm>
#include <queue>
#include <vector>
#include <stack>
#include <map>
#include <set>
#include <sstream>
#include <iomanip>
#include <cmath>
#include <bitset>
#include <assert.h>
#include <unordered_map>

using namespace std;
typedef long long ll;

#define Cmp(a, b) memcmp(a, b, sizeof(b))
#define Cpy(a, b) memcpy(a, b, sizeof(b))
#define Set(a, v) memset(a, v, sizeof(a))
#define debug(x) cout << #x << ": " << x << endl
#define _forS(i, l, r) for(set<int>::iterator i = (l); i != (r); i++)
#define _rep(i, l, r) for(int i = (l); i <= (r); i++)
#define _for(i, l, r) for(int i = (l); i < (r); i++)
#define _forDown(i, l, r) for(int i = (l); i >= r; i--)
#define debug_(ch, i) printf(#ch"[%d]: %d\n", i, ch[i])
#define debug_m(mp, p) printf(#mp"[%d]: %d\n", p->first, p->second)
#define debugS(str) cout << "dbg: " << str << endl;
#define debugArr(arr, x, y) _for(i, 0, x) { _for(j, 0, y) printf("%c", arr[i][j]); printf("\n"); }
#define _forPlus(i, l, d, r) for(int i = (l); i + d < (r); i++)
#define lowbit(i) (i & (-i))
#define MPR(a, b) make_pair(a, b)

pair<int, int> crack(int n) {
    int st = sqrt(n);
    int fac = n / st;
    while (n % st) {
        st += 1;
        fac = n / st;
    }

    return make_pair(st, fac);
}

inline ll qpow(ll a, int n) {
    ll ans = 1;
    for(; n; n >>= 1) {
        if(n & 1) ans *= 1ll * a;
        a *= a;
    }
    return ans;
}

template <class T>
inline bool chmax(T& a, T b) {
    if(a < b) {
        a = b;
        return true;
    }
    return false;
}

ll gcd(ll a, ll b) {
    return b == 0 ? a : gcd(b, a % b);
}

ll ksc(ll a, ll b, ll mod) {
    ll ans = 0;
    for(; b; b >>= 1) {
        if (b & 1) ans = (ans + a) % mod;
        a = (a * 2) % mod;
    }
    return ans;
}

ll ksm(ll a, ll b, ll mod) {
    ll ans = 1 % mod;
    a %= mod;

    for(; b; b >>= 1) {
        if (b & 1) ans = ksc(ans, a, mod);
        a = ksc(a, a, mod);
    }

    return ans;
}

template <class T>
inline bool chmin(T& a, T b) {
    if(a > b) {
        a = b;
        return true;
    }
    return false;
}

template<class T>
bool lexSmaller(vector<T> a, vector<T> b) {
    int n = a.size(), m = b.size();
    int i;
    for(i = 0; i < n && i < m; i++) {
        if (a[i] < b[i]) return true;
        else if (b[i] < a[i]) return false;
    }
    return (i == n && i < m);
}

// ============================================================== //

const int maxn = 200 + 10, maxm = (maxn + 40000) * 2;
const int inf = 0x3f3f3f3f;
int head[maxn], ver[maxm], e[maxm], w[maxm], ne[maxm], idx = 1;
int n, m, S, T, K;

void add(int a, int b, int c) {
    ver[++idx] = b; w[idx] = c; ne[idx] = head[a]; head[a] = idx;
    ver[++idx] = a; w[idx] = c; ne[idx] = head[b]; head[b] = idx;
}

int d[maxn], cur[maxn];
bool bfs() {
    memset(d, -1, sizeof d);
    d[S] = 0, cur[S] = head[S];
    queue<int> q; q.push(S);

    while (q.size()) {
        int x = q.front(); q.pop();
        for (int i = head[x]; i; i = ne[i]) {
            int y = ver[i];
            if (d[y] == -1 && e[i]) {
                d[y] = d[x] + 1;
                cur[y] = head[y];
                if (y == T) return true;
                q.push(y);
            }
        }
    }
    return false;
}

int dinic(int u, int lim) {
    if (u == T) return lim;
    int flow = 0;
    for (int i = cur[u]; i && lim > flow; i = ne[i]) {
        cur[u] = i;
        int v = ver[i];
        if (d[v] == d[u] + 1 && e[i]) {
            int t = dinic(v, min(e[i], lim-flow));
            if (!t) d[v] = -1;
            flow += t, e[i] -= t, e[i^1] += t;
        }
    }
    return flow;
}

int dinic() {
    int res = 0, flow;
    while (bfs()) while (flow = dinic(S, inf)) res += flow;
    return res;
}

bool check(int x) {
    for (int i = 2; i <= idx; i++) {
        if (w[i] > x) e[i] = 0;
        else e[i] = 1;
    }
    return dinic() >= K;
}

void solve() {
    int l = 1, r = 1e6;
    while (l < r) {
        int mid = (l + r) >> 1;
        if (check(mid)) r = mid;
        else l = mid + 1;
    }
    printf("%d\n", l);
}

int main() {
    freopen("input.txt", "r", stdin);
    scanf("%d%d%d", &n, &m, &K);
    S = 1, T = n;
    for (int i = 0; i < m; i++) {
        int a, b, c;
        scanf("%d%d%d", &a, &b, &c);
        add(a, b, c);
    }

    // then solve
    solve();
}