题目描述

直方图是由在公共基线处对齐的一系列矩形组成的多边形。

矩形具有相等的宽度，但可以具有不同的高度。

例如，图例左侧显示了由高度为 2,1,4,5,1,3,3 的矩形组成的直方图，矩形的宽度都为 1：

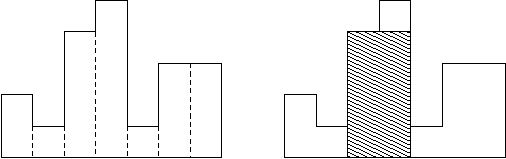
通常，直方图用于表示离散分布，例如，文本中字符的频率。

现在，请你计算在公共基线处对齐的直方图中最大矩形的面积。

图例右图显示了所描绘直方图的最大对齐矩形。

算法1

单调栈

首先在数组的首尾各增加一个-1的值，这样就不需要判断栈是否为空，因为栈中始终会有-1的值。
其次关注每个高度的左边界：栈存放数组下标，当栈顶对应的高度大于等于当前高度时，出栈并指向下一个更低的高度。循环最后得到距离最近的比当前高度小的值所在的下标，存入l数组；
右边界同理。

C++ 代码

#include <iostream>
#include <stack>

using namespace std;
const int N = 100010;
int h[N], l[N], r[N];

stack<int> stk;

int main(){
    int n;
    while(cin >>n, n){
        for(int i = 1; i<=n; i++) cin >> h[i];
        h[0] = h[n+1] = -1;

        //求左边界
        stk.push(0);
        for(int i=1; i<=n; i++){
            while(h[stk.top()] >= h[i]) stk.pop();
            l[i] = stk.top();  //最近的比当前高度低的值对应的下标
            stk.push(i);
        }

        while(!stk.empty()) stk.pop(); //empty the stack

        //求右边界
        stk.push(n+1);
        for(int i=n; i>0; i--){
            while(h[stk.top()] >= h[i]) stk.pop();
            r[i] = stk.top();
            stk.push(i);
        }

        long long res = 0;
        for(int i=1; i<=n; i++){
            res = max(res, (long long) h[i]*(r[i]-l[i]-1));
        }
        cout << res << endl;

    }
    return 0;
}