栈

时间复杂度：$O(N)$

该题可见 2022王道考研 数据结构-栈的应用 这一节，讲的十分清晰。

题目所给的为中缀表达式，我们需将中缀表达式利用栈转为后缀表达式，因为计算机对后缀表达式的处理会更加容易，再利用栈计算后缀表达式，得到最后的结果。

由此我们可以利用双栈，即在转换为后缀表达式同时计算后缀表达式的结果，一个栈存储运算符，一个栈存储操作数，具体的运算规则（例子）来自 《2022 王道考研-数据结构》。

思路：

顺序扫描中缀表达式中的每一项，若是操作数或'('则直接压入栈中，若是')'，则在运算符栈中弹出运算符直至 ')'参与运算，若是运算符，则在运算符栈中弹出优先级 >= 当前运算符中的所有运算符参与运算，最后对运算符栈剩余运算符全部参与运算即可，剩下的操作数栈剩下的一个数即为答案。

举例：

中缀表达式：A+B*(C-D)-E/F
后缀表达式：ABCD-*+EF/-

下图是对后缀表达式（略去了中缀 –> 后缀）的处理流程：

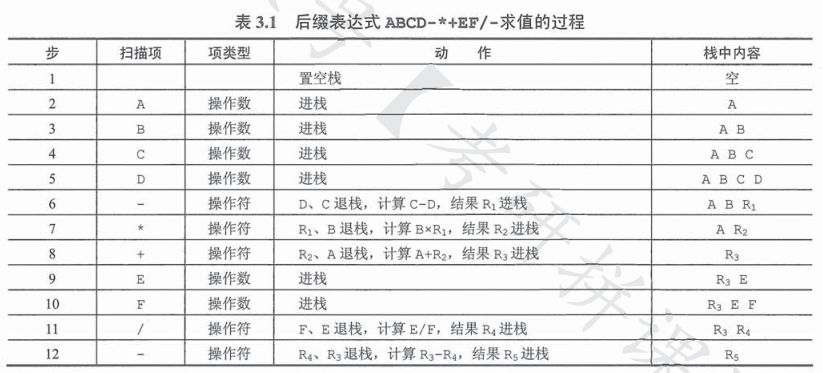
C++ 代码

#include <iostream>
#include <algorithm>
#include <unordered_map>
#include <cstring>
#include <stack>
#include <ctype.h>
using namespace std;

string s;
stack <int> num; // 操作数
stack <char> op; // 运算符

void eval()
{
    int b = num.top(); num.pop();
    int a = num.top(); num.pop();
    int c;
    char x = op.top(); op.pop();
    if (x == '+') c = a + b;
    else if (x == '-') c = a - b;
    else if (x == '*') c = a * b;
    else c = a / b;
    num.push(c);
}

int main()
{
    cin >> s;
    unordered_map<char, int> pri{{'+', 1}, {'-', 1}, {'*', 2}, {'/', 2}}; // 定义运算符优先级
    for (int i = 0; i < s.size(); ++i) {
        if (isdigit(s[i])) {
            int x = 0, j = i;
            while (j < s.size() && isdigit(s[j])) {
                x = x * 10 + s[j++] - '0';
            }
            i = j - 1;
            num.push(x);
        }
        else if (s[i] == '(') op.push('(');
        else if (s[i] == ')') {
            while (op.top() != '(') {
                eval();
            }
            op.pop();
        }
        else {
            while (op.size() && pri[op.top()] >= pri[s[i]]) {
                eval();
            }
            op.push(s[i]);
        }
    }
    while (op.size()) eval();
    cout << num.top() << endl;
    return 0;
}