解法一

之前的解法有问题, 被Hack了。下面是正确解法

package main

import (
    "bufio"
    "container/heap"
    "fmt"
    "os"
    "strconv"
    "strings"
)

var price []int
var rank []int
var w [][]int
var INF = int(0x3f3f3f3f)

func main() {
    // f, _ := os.Open("./input.txt")
    // reader := bufio.NewReader(f)
    reader := bufio.NewReader(os.Stdin)
    // writer := bufio.NewWriter(os.Stdout)
    t := ReadArray(reader)
    M, N := t[0], t[1]
    rank = make([]int, N+1)
    w = make([][]int, N+1)
    for i := 0; i <= N; i++ {
        w[i] = make([]int, N+1)
        for j := 0; j <= N; j++ {
            w[i][j] = INF
        }
    }
    for i := 1; i <= N; i++ {
        plx := ReadArray(reader)
        rank[i] = plx[1]
        // 虚拟源点，连接所有节点
        w[0][i] = plx[0]
        for j := 0; j < plx[2]; j++ {
            tv := ReadArray(reader)
            // 反向建边
            w[tv[0]][i] = tv[1]
        }
    }
    var res = INF
    // 枚举区间 [rank[1]-m, rank[1]+m]
    for i := rank[1] - M; i <= rank[1]; i++ {
        res = Min(res, Dijkstra(N, i, i+M))
    }
    fmt.Println(res)
}

func Dijkstra(n int, lt int, rt int) int {
    pq := make(NodeHeap, 0)
    vis := make([]bool, n+1)
    dis := make([]int, n+1)
    for i := 0; i <= n; i++ {
        dis[i] = INF
    }
    heap.Push(&pq, &Node{
        idx: 0,
        val: 0,
    })
    dis[0] = 0
    for len(pq) > 0 {
        cur := heap.Pop(&pq).(*Node)
        i, v := cur.idx, cur.val
        if vis[i] {
            continue
        }
        vis[i] = true
        for j := 1; j <= n; j++ {
            if rank[j] > rt || rank[j] < lt {
                continue
            }
            if w[i][j] == INF {
                continue
            }
            if w[i][j]+v < dis[j] {
                dis[j] = w[i][j] + v
                heap.Push(&pq, &Node{j, dis[j]})
            }
        }
    }
    return dis[1]
}

func Min(a, b int) int {
    if a < b {
        return a
    }
    return b
}

type Node struct {
    idx int
    val int
}

type NodeHeap []*Node

func (h NodeHeap) Len() int { return len(h) }

// 小顶堆
func (h NodeHeap) Less(i, j int) bool { return h[i].val < h[j].val }
func (h NodeHeap) Swap(i, j int)      { h[i], h[j] = h[j], h[i] }

func (h *NodeHeap) Push(x interface{}) {
    // Push 和 Pop 使用 pointer receiver 作为参数，
    // 因为它们不仅会对切片的内容进行调整，还会修改切片的长度。
    *h = append(*h, x.(*Node))
}

func (h *NodeHeap) Pop() interface{} {
    old := *h
    n := len(old)
    x := old[n-1]
    *h = old[0 : n-1]
    return x
}

func ReadLine(reader *bufio.Reader) string {
    line, _ := reader.ReadString('\n')
    return strings.TrimRight(line, "\n")
}

func ReadInt(reader *bufio.Reader) int {
    num, _ := strconv.Atoi(ReadLine(reader))
    return num
}

func ReadArray(reader *bufio.Reader) []int {
    line := ReadLine(reader)
    strs := strings.Split(line, " ")
    nums := make([]int, len(strs))
    for i, s := range strs {
        nums[i], _ = strconv.Atoi(s)
    }
    return nums
}

错误解法示例

这里的解法是错的，每个节点可能在多条路径上，所以这里统计路径上的最大最小rank是不准确的，每个点都可能被松弛多次，并不能保证维护的一定是最短路上的max，min

建图的时候直接建立当前物品和其替代品的边。记录每个物品的价格$price$和主人等级$rank$

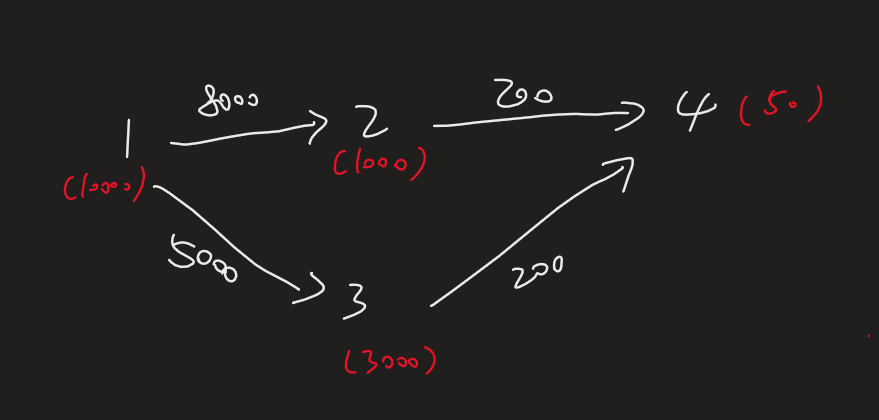
优先队列中存储节点的编号$i$，当前离物品$1$（公主）的最短路$v$，以及路径上的最大等级$max$和最小等级$min$，在松弛的时候判断等级有没有超过限制，并且维护这两个值，然后在优先队列弹出节点的时候统计最小值（弹出节点的最短路已经确定了，尝试在当前节点停止替换操作，直接原价购买）

import java.util.*;
import java.io.*;

class Main {

    static class Node {
        int i, v;
        int max, min;
        public Node(int i, int v, int max, int min) {
            this.i = i; this.v = v;
            this.max = max; this.min = min;
        }
    }

    public static void main(String... args) throws Exception {
        PrintWriter out = new PrintWriter(new BufferedOutputStream(System.out));
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        // BufferedReader br = new BufferedReader(new InputStreamReader(new FileInputStream("./input.txt")));
        int[] in = read(br);
        int INF = 0x3f3f3f3f;
        int M = in[0], N = in[1];
        int[][] w = new int[N+1][N+1];
        for (int i = 1; i <= N; i++) {
            Arrays.fill(w[i], INF);
        }
        // 记录每个物品的价格和主人等级
        int[] price = new int[N+1];
        int[] rank = new int[N+1];
        for (int i = 1; i <= N; i++) {
            int[] plx = read(br);
            price[i] = plx[0]; rank[i] = plx[1];
            for (int j = 1; j <= plx[2]; j++) {
                int[] tv = read(br);
                w[i][tv[0]] = tv[1];
            }
        }
        int res = INF;
        int[] dis = new int[N+1];
        boolean[] vis = new boolean[N+1];
        // pq 中存储节点的编号，以及路径上的最大和最小等级
        PriorityQueue<Node> pq = new PriorityQueue<>((a,b)->a.v-b.v);
        Arrays.fill(dis, INF);
        dis[1] = 0; pq.add(new Node(1, 0, rank[1], rank[1]));
        while (!pq.isEmpty()) {
            Node node = pq.poll();
            int i = node.i, v = node.v;
            if (vis[i]) continue;
            vis[i] = true;
            // 在当前位置停止替换
            res = Math.min(res, dis[i]+price[i]);
            for (int j = 1; j <= N; j++) {
                if (w[i][j] == INF) continue;
                // 等级限制无法交易
                if (Math.abs(rank[j]-node.min) > M || 
                    Math.abs(rank[j]-node.max) > M ) continue; 
                if (dis[j] > v + w[i][j]) {
                    dis[j] = v + w[i][j];
                    pq.add(new Node(j, dis[j], Math.max(rank[j], node.max), Math.min(rank[j], node.min)));
                }
            }
        }
        out.println(res);
        out.flush();
    }

    public static int[] read(BufferedReader br) throws Exception {
        return Arrays.stream(br.readLine().split(" ")).mapToInt(Integer::parseInt).toArray();
    }
}