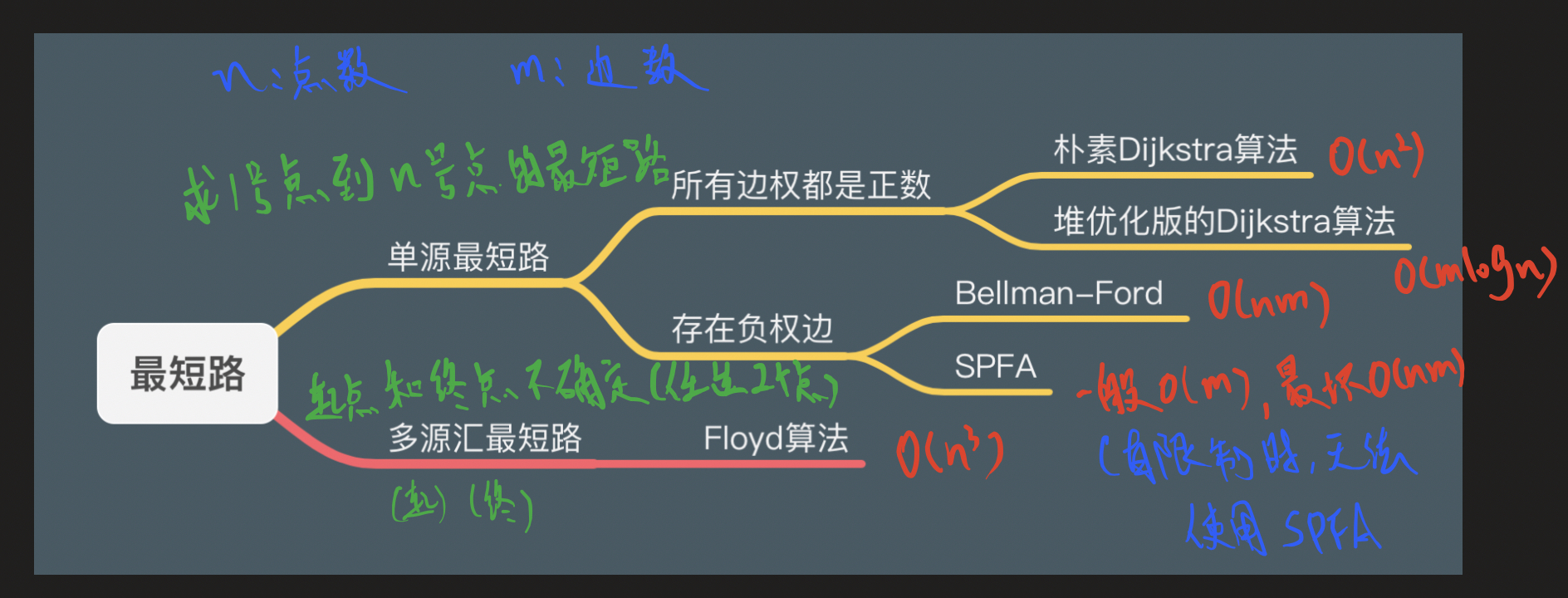
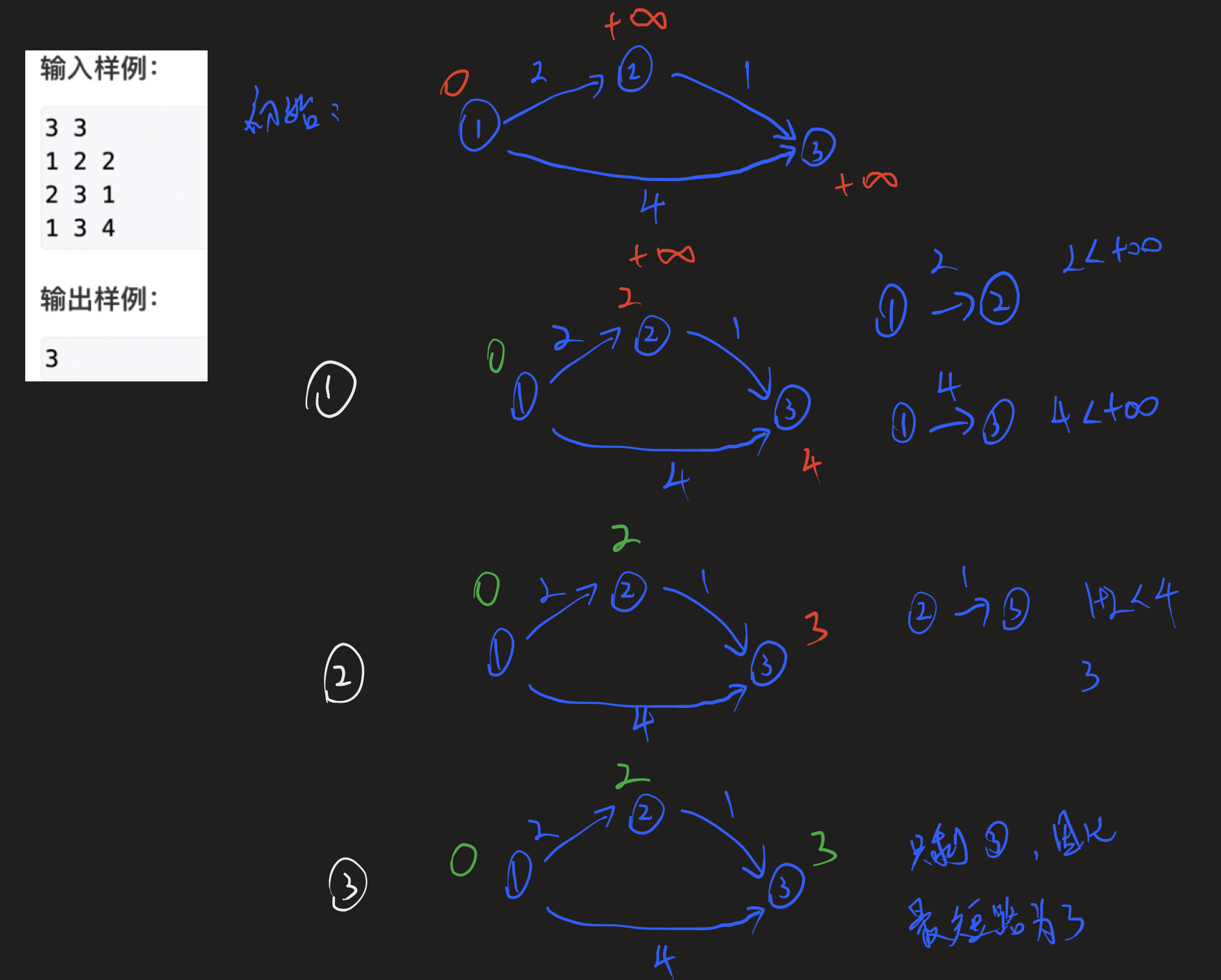
代码

#include <algorithm>
#include <cstring>
#include <iostream>

using namespace std;

const int N = 5e2 + 10;

int n, m;
int g[N][N];  //邻接矩阵
int dist[N];  //从1号点走到每个点， 当前的最短距离是多少
bool st[N];  //用于在更新最短距离时，判断当前的点的最短距离是否确定，是否需要更新

// 进行n次迭代后最后就可以确定每个点的最短距离
// 然后再根据题意输出相应的 要求的最短距离
int dijkstra()
{
    memset(dist, 0x3f, sizeof dist);
    dist[1] = 0;  // 第一个点到自己的距离为0

    for (int i = 0; i < n - 1; i++) {  //遍历n-1轮， 每轮确定一个点（从1到该点的最短路径
        int t = -1;
        // 找到未标记节点中， dist最小的
        for (int j = 1; j <= n; j++) {
            if (!st[j] && (t == -1 || dist[t] > dist[j])) {
                t = j;
            }
        }

        // 用全局最小值点t更新其他节点
        for (int j = 1; j <= n; j++) {
            dist[j] = min(dist[j], dist[t] + g[t][j]);  //t->j
        }

        // t代表就是剩余未确定最短路的点中 路径最短的点
        st[t] = true;  // 而与此同时该点的最短路径也已经确定我们将该点标记
    }

    if (dist[n] == 0x3f3f3f3f) {  // 如果第n个点路径为无穷大即不存在最低路径
        return -1;
    }
    return dist[n];
}

int main()
{
    cin >> n >> m;

    memset(g, 0x3f, sizeof g);

    for (int i = 0; i < m; i++) {
        int a, b, c;
        cin >> a >> b >> c;
        g[a][b] = min(g[a][b], c);  // 如果发生重边的情况则保留最短的一条边
    }

    // 求单源最短路径
    cout << dijkstra() << endl;

    return 0;
}