从后序中序遍历 构造树

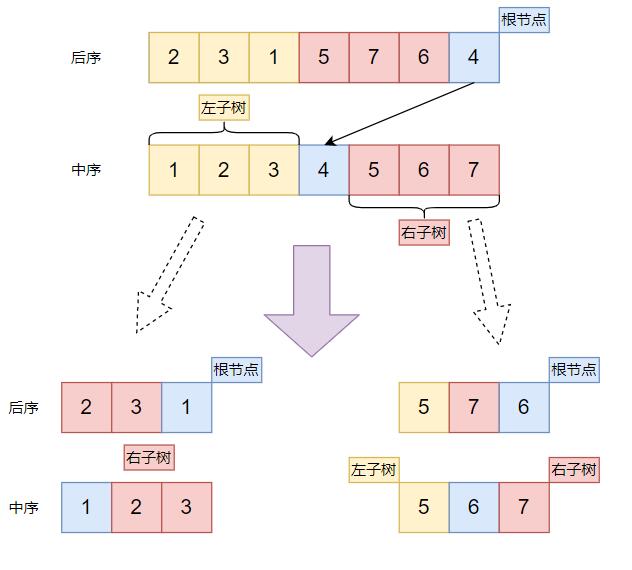
后序遍历最后一位必定是当前区间节点的根，除去最后一位剩余的区间可分为不重叠的两部分，依次为左子树、右子树 （某一子树可能为空 则有一部分什么节点都没有）

中序遍历必定存在一个节点为当前区间的根，其左侧所有元素属于左子树，右侧所有元素属于右子树 （某一子树可能为空 则仅有一侧）

因此先通过后序遍历的最后一个元素确定区间的根节点，
再从中序遍历中找出根节点的位置，划分区间为左右子树
根据左子树的元素个数，在后序遍历中划分出左右子树两部分
从而得到两个新的区间（包含了对应的后序遍历和中序遍历），递归上述步骤求解新的区间直到找到所有叶子节点

代码实现时，只需用两个HashMap分别记录根节点对应的左右节点，所有节点记录完则树的构造结束

层序遍历 可以视为以根节点开始的BFS 直到遍历完所有节点

import java.util.*;
import java.lang.*;

public class Main {
    static Scanner scanner = new Scanner(System.in);

    static int n, N = 31;
    static int[] back = new int[N], middle = new int[N];
    static HashMap<Integer, Integer> leftChild = new HashMap<>();
    static HashMap<Integer, Integer> rightChild = new HashMap<>();

    static int dfs(int l1, int r1, int l2, int r2) {
        if (l2 > r2 || l2 < 1 || r2 > n) return -1;  // 退出条件 找不到已知的子节点
        int root = back[r1];  // 后序遍历的最后一位是根节点
        int pos;  // 在中序遍历找根节点的位置
        for (pos = l2; pos <= r2 && middle[pos] != root; pos++) ;
        int leftLen = pos - l2;  // 计算左子树的长度
        leftChild.put(root, dfs(l1, l1 + leftLen - 1, l2, pos - 1));  // 递归左子树区间
        rightChild.put(root, dfs(l1 + leftLen, r1 - 1, pos + 1, r2));  // 递归右子树区间
        return root;  // 返回区间根节点
    }

    public static void main(String[] args) {
        n = scanner.nextInt();
        for (int i = 1; i <= n; i++) back[i] = scanner.nextInt();
        for (int i = 1; i <= n; i++) middle[i] = scanner.nextInt();
        int root = dfs(1, n, 1, n);  // 返回是区间[1,n]的根节点 即整棵树

        StringBuilder sb = new StringBuilder();  // 存答案
        ArrayDeque<Integer> que = new ArrayDeque<>();  // BFS
        que.addLast(root);  // 根节点入队
        while (!que.isEmpty()) {
            Integer node = que.removeFirst();
            sb.append(node).append(" ");
            int left = leftChild.get(node), right = rightChild.get(node);
            if (left != -1) que.addLast(left);  // 如果有左子树 子节点入队
            if (right != -1) que.addLast(right);  // 如果有右子树 子节点入队
        }
        System.out.println(sb);
    }
}