题目描述

观察这个数列：

1 3 0 2 -1 1 -2 …

这个数列中后一项总是比前一项增加2或者减少3，且每一项都为整数。

栋栋对这种数列很好奇，他想知道长度为 n 和为 s 而且后一项总是比前一项增加 a 或者减少 b 的整数数列可能有多少种呢？

输入格式
共一行，包含四个整数 n,s,a,b，含义如前面所述。

输出格式
共一行，包含一个整数，表示满足条件的方案数。

由于这个数很大，请输出方案数除以 100000007 的余数。

数据范围
1≤n≤1000,
−109≤s≤109,
1≤a,b≤106
输入样例：

4 10 2 3

输出样例：

2

样例解释
两个满足条件的数列分别是2 4 1 3和7 4 1 -2。

波动数列

刚看完y总的讲解 内心os: 牛啊,牛啊
思路:

• 从序列问题转化为组合问题

• 根据背包问题模型求解

转化分析:

• 我们假设这个序列的第一个数是x,设 $d_i$ 是增加或减少的那个数,s为和,那么这个序列可以表示成这样
  $$ x, x + d_1, x + d_1 + d_2, x + d_1 + d_2 + d_3, ...., x + d_1 + d_2 + .... + d_{n-1} $$

• 将上式做加法所得即为s
  $$ x + x + d_1 + x + d_1 + d_2 + x + d_1 + d_2 + d_3 + .... + x + d_1 + d_2 + .... + d_{n-1} = s$$
  上式进行同类型合并得
  $$ n · x + (n-1)· d_1 + (n-2) ·d_2 + ...... + 1 · d_{n-1} = s$$

• 由于x的取值用很多种情况，而 $d_i$ 的取值只有 $+a$ 或 $-b$两种情况， 但是上式为等式，这样就可以将x具体化
  $$ x = \frac{s - (n-1)· d_1 - (n-2) ·d_2 - ...... - 1 · d_{n-1}}{n} $$

• 可以看出每一组$d_{1}$ ~ $d_{n}$的取值对应一组序列，反过来也同样对应,$ d_i $ 的每一种取法就对应了一个序列
  那么这个题就转化成了求满足要求的组合而这个要求分为两个，①：$ d_i $ 有两种取值要么 $-a$ 要么 $+b$ ②：由于x是整数那么就要求$s - (n-1)· d_1 - (n-2) ·d_2 - ...... - 1 · d_{n-1}$ 是n的倍数即%n = 0在换句话说就是 $(n-1)· d_1 + (n-2) ·d_2 + ...... + 1 · d_{n-1}$ 与s同余

• 经过上面的转化我们要做的就是求满足要求的数量了

dp分析:
闫氏dp分析法来一套

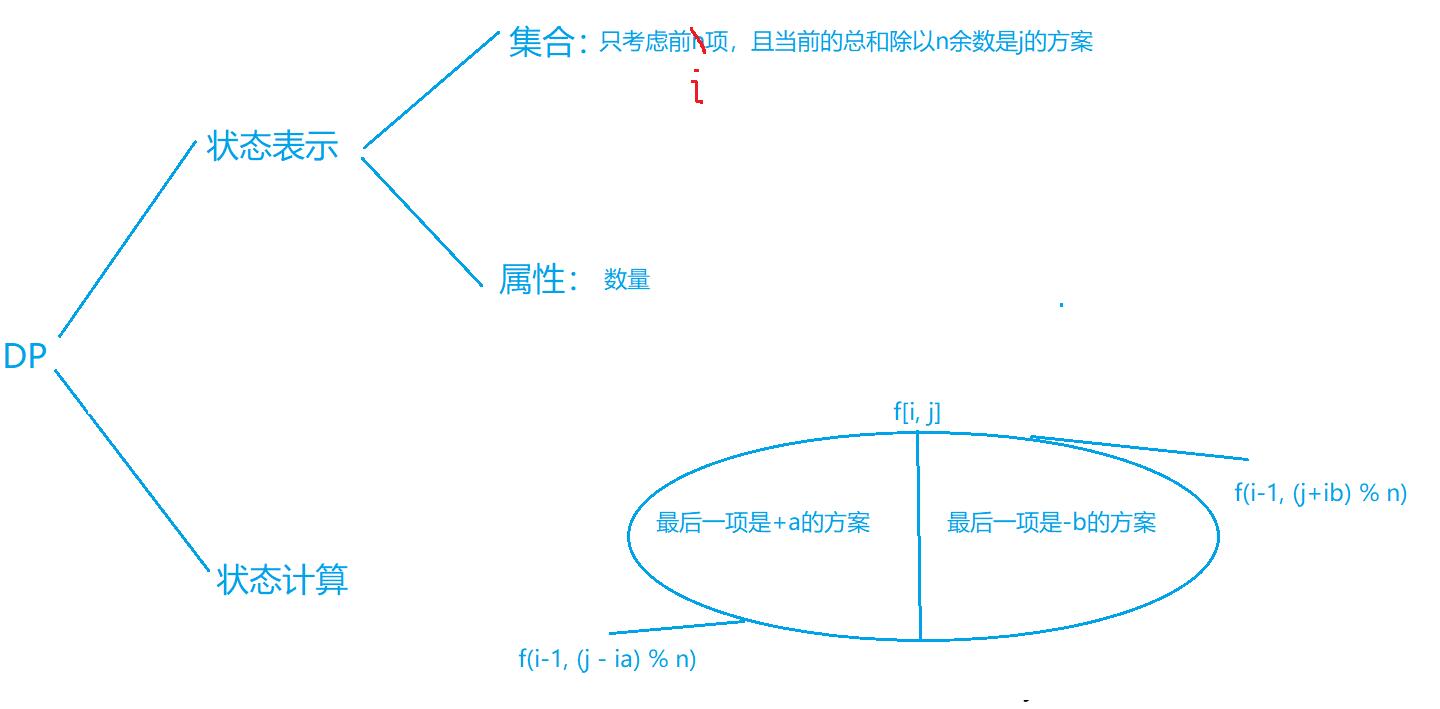
• 这里有个小技巧：$(n-1)· d_1 + (n-2) ·d_2 + ...... + 1 · d_{n-1}$ 与 $ 1 · d_1 + 2 ·d_2 + .... + (n-1) · d_{i-1}$ 是一个意思

• 所以根据状态表示在第 $i$ 处 可以表示为 f[i-1,c + i·a] 即 $c + i·a$ 同余 $j$所以 $c$ 同余 $j - i·a$

至此分析完毕, 上代码

c++代码

#include <iostream>
#include <algorithm>

using namespace std;
const int N = 1010, mod = 1e8+7;

int f[N][N];

int get_mod(int a,int b){
    return (a % b + b) % b;
}

int main()
{
    int n, s, a, b;
    cin >> n >> s >> a >> b;
    f[0][0] = 1;
    for(int i = 1; i < n; i ++ )
        for(int j = 0; j < n; j ++ )
            f[i][j] = (f[i - 1][get_mod(j - a*(n - i),n)] + f[i - 1][get_mod(j + b * (n - i), n)]) % mod;

    cout << f[n - 1][get_mod(s, n)] << endl;

    return 0;
}