题目描述

X 国王有一个地宫宝库，是 n×m 个格子的矩阵，每个格子放一件宝贝，每个宝贝贴着价值标签。

地宫的入口在左上角，出口在右下角。

小明被带到地宫的入口，国王要求他只能向右或向下行走。

走过某个格子时，如果那个格子中的宝贝价值比小明手中任意宝贝价值都大，小明就可以拿起它（当然，也可以不拿）。

当小明走到出口时，如果他手中的宝贝恰好是 k 件，则这些宝贝就可以送给小明。

请你帮小明算一算，在给定的局面下，他有多少种不同的行动方案能获得这 k 件宝贝。

输入格式
第一行 3 个整数，n,m,k，含义见题目描述。

接下来 n 行，每行有 m 个整数 Ci 用来描述宝库矩阵每个格子的宝贝价值。

输出格式
输出一个整数，表示正好取 k 个宝贝的行动方案数。

该数字可能很大，输出它对 1000000007 取模的结果。

数据范围
$1≤n,m≤50$
$1≤k≤12$
$0≤Ci≤12$
输入样例1：

2 2 2
1 2
2 1

输出样例1：

2

输入样例2：

2 3 2
1 2 3
2 1 5

输出样例2：

14

地宫取宝

做法：四维dp

• 第一次接触高维dp，穿插一个小tips，遇到高维dp不要怕，只不过是要考虑的情况变多而已，这个题虽然麻烦但却不难

• 思考时有一个误区，就是没把c给考虑成一维，一直在设法判断c的取值，其实只需将c也考虑为一维,循环一遍从(0~c)即可

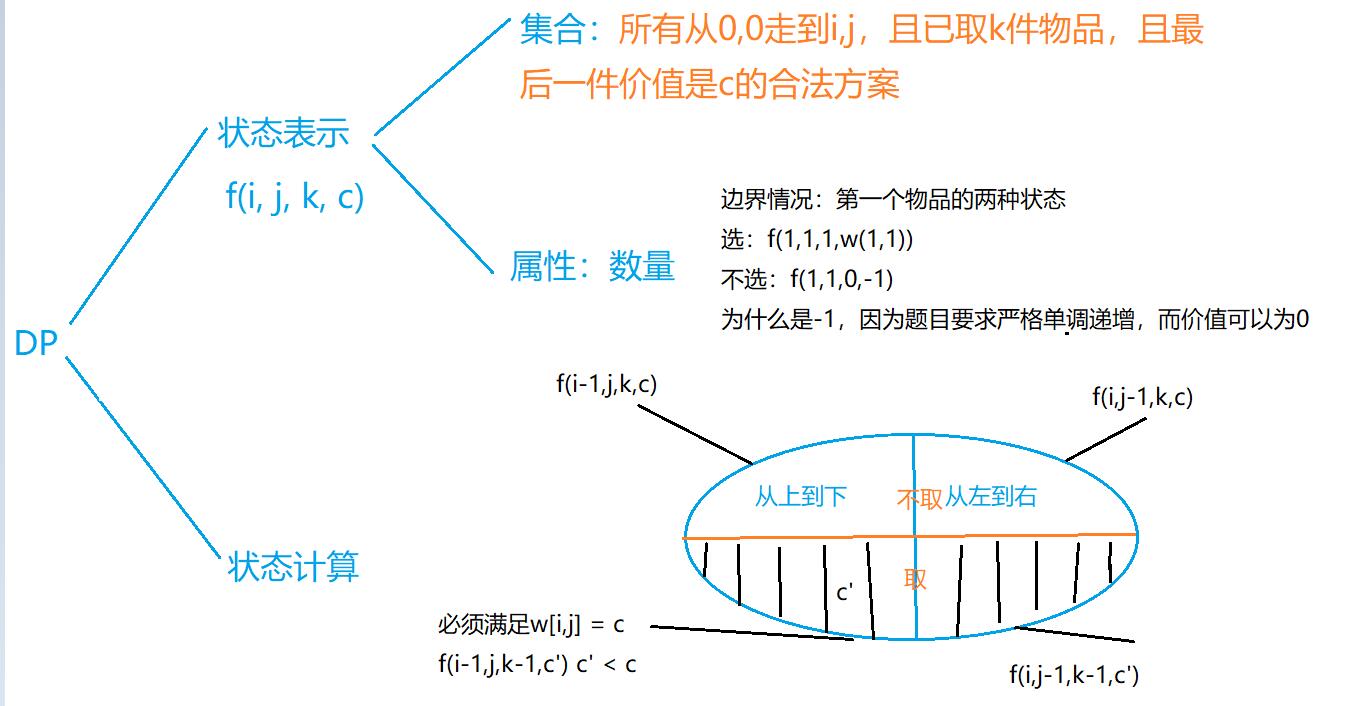
分析:

• 这题其实可以既像背包问题,又像线性dp,根据之前做过的摘花生这个题大致可以考虑出像背包的部分,只可以往下和往右走和这个点取或不取，分为f[i-1][j][k-1][c]&f[i-1][j][k][c]&f[i][j-1][k][c]&f[i][j-1][k-1][c]这一步很简单 i,j 为方向问题, k 为取或不取问题

• 个人觉得最难得是c的判定，这个题我觉得这个c的判定其实就是根据经验了，因为题目里有有关于c的要求，所以第四维的c起到一个判断方案是否合法的作用

• 这种麻烦的题,练的少,考试根本做不出

#include <iostream>
#include <algorithm>

using namespace std;
const int N = 60, mod = 1e9 + 7;

int n, m, k;
int w[N][N];
int f[N][N][13][14];

int main()
{
    cin >> n >> m >> k;

    for(int i = 1; i <= n; i ++ )
        for(int j = 1; j <= m; j ++ )
        {
            cin >> w[i][j];
            //由于我们在第一个点的时候可取或不取，取为w[i][j]不取为-1,但数组下标没有-1,所以总体++，不影响最后结果
            w[i][j] ++;
        }    

    //边界情况初始化
    f[1][1][1][w[1][1]] = 1;
    f[1][1][0][0] = 1;

    for(int i = 1; i <= n; i ++ )
        for(int j = 1; j <= m; j ++ )
        {
            if(i == 1 && j == 1) continue;
            for(int u = 0; u <= k; u ++ )
                for(int v = 0; v <= 13 ;v ++ )
                {
                    int &val = f[i][j][u][v];
                    val = (val + f[i - 1][j][u][v]) % mod;
                    val = (val + f[i][j - 1][u][v]) % mod;
                    if(u > 0 && v == w[i][j]) 
                    {
                        for(int c = 0; c < v; c ++ )
                        {
                            val = (val + f[i - 1][j][u - 1][c]) % mod;
                            val = (val + f[i][j - 1][u - 1][c]) % mod;
                        }
                    }
                }
        }

    int res = 0;
    //找第k件物品可能价值的所有答案，并求和为最后答案
    for(int i = 0; i <= 13; i ++ ) res = (res + f[n][m][k][i]) % mod;

    printf("%d", res);

    return 0;
}