循环流与具有下界的流
$\text{[2020]}\quad \text{Douglas B.West, Introduction to Graph Theroy, Second Edition(图论导引 原书第二版)}$
$\text{chapter 4},\ \textbf{定理4.3.20}$

• 原网络 $G$ 添加从 $t \to s$ 的具有 $+\infty$ 容量的边，此时的网络有个处处守恒的可行流
  称为循环流

• 对于可行循环流 $C$，在所有节点处引入供应量 $\sigma (x_i)$ 和需求量 $\partial (x_i)$，给定流量约束
  $l(e) \leqslant f(e) \leqslant u(e)$，在每一条边上令 $c(e) = u(e) - l(e)$
  $f^{+}(v)$ 表示离开 $v$ 的总流量，$f^{-}(v)$ 表示进入 $v$ 的总流量
  $$\begin{gathered} l^{-}(v) = \sum_{e \in [V(C)-v, v]} l(e) \\\ l^{+}(v) = \sum_{e \in [v, V(C)-v]} l(e) \\\ b(v) = l^{-}(v) - l^{+}(v) \end{gathered}$$
  $$\cdots \xrightarrow{l^{-}(v)} v \xrightarrow{l^{+}(v)} \cdots$$

• 由于可行循环流流量处处守恒，所以 $\sum b(v) = 0$，一个循环可行流在每个顶点满足
  $f^{+}(v) - f^{-}(v) = 0$，令 $f’(e) = f(e) - l(e)$
  $$\begin{cases} f’^{+}(v) = f^{+}(v) - l^{+}(v) \\\ f’^{-}(v) = f^{-}(v) - l^{-}(v) \end{cases}$$
  可以推出
  $$\begin{cases} l’^{-}(v) = f^{-}(v) - f’^{-}(v) \\\ l’^{+}(v) = f^{+}(v) - f’^{+}(v) \end{cases} \xrightarrow{f^{+}(v) = f^{-}(v)}$$
  所以有
  $$l^{-}(v) - l^{+}(v) = b(v) = f’^{+}(v) - f’^{-}(v)$$
  也就是说，$f$ 是 $C$ 中的一个可行流当且仅当
  $f’$ 满足流量约束 $0 \leqslant f’(e) \leqslant c(e)$
  并且在每个顶点处满足 $f’^{+}(v) - f’^{-}(v) = b(v)$

• 这样可以将循环流问题转换为一个供应量和需求量的问题，为了满足流量守恒，需要这样做

• $b(v) \geqslant 0$，那么 $v$ 向网络供应流量 $|b(v)|$
  建立一个超级源点 $S$，令容量 $c(S, v) = |b(v)|$

• $b(v) < 0$，则 $v$ 对网络有 $|b(v)|$ 的需求量
  建立一个超级汇点 $T$，$c(v, T) = |b(v)|$

• 这样我们构造出了新网络 $G$，并且之前已经证明了
  $C$ 有一个可行循环流 $f$ 当且仅当 $G$ 有一个满流浸润了离开 $S$ 或进入 $T$ 的所有边
  此时我们称 $G$ 保持一个浸润状态

$\textbf{algorithm}$

• 根据上述方法在原网络 $G$ 的基础上，建立超级源点 $S$ 和 超级汇点 $T$，来满足供需关系

• 在原网络 $G$ 的汇点 $t$ 和 源点 $s$ 中，连一条边使得 $c(t, s) = +\infty$
  此时构造出可行循环流网络，新网络记为 $N$

• $\textbf{dinic}(N)$ 判断新网络是否浸润

• 如果浸润，在浸润状态下 $N$ 的一个可行流记为 $f_0$
  那么 $f_0$ 中从 $s \to t$ 的流量 $f_0(s \to t) = e(t \to s)$
  $e(t \to s)$ 表示执行完 $\textbf{dinic}$ 之后，边 $(t, s)$ 的容量

• 去掉循环流的边 $(t, s)$，再次执行 $\textbf{dinic}$ 算法，使得 $s \to t$ 没有增广路
  $f’ = \textbf{dinic}(s, t)$，表示执行增广能够增加的流量为 $f’$
  则此时 $(f_0 \uparrow f’) = f$，$f$ 即为 $s \to t$ 的上下界最大流

下面来证明这个算法的正确性


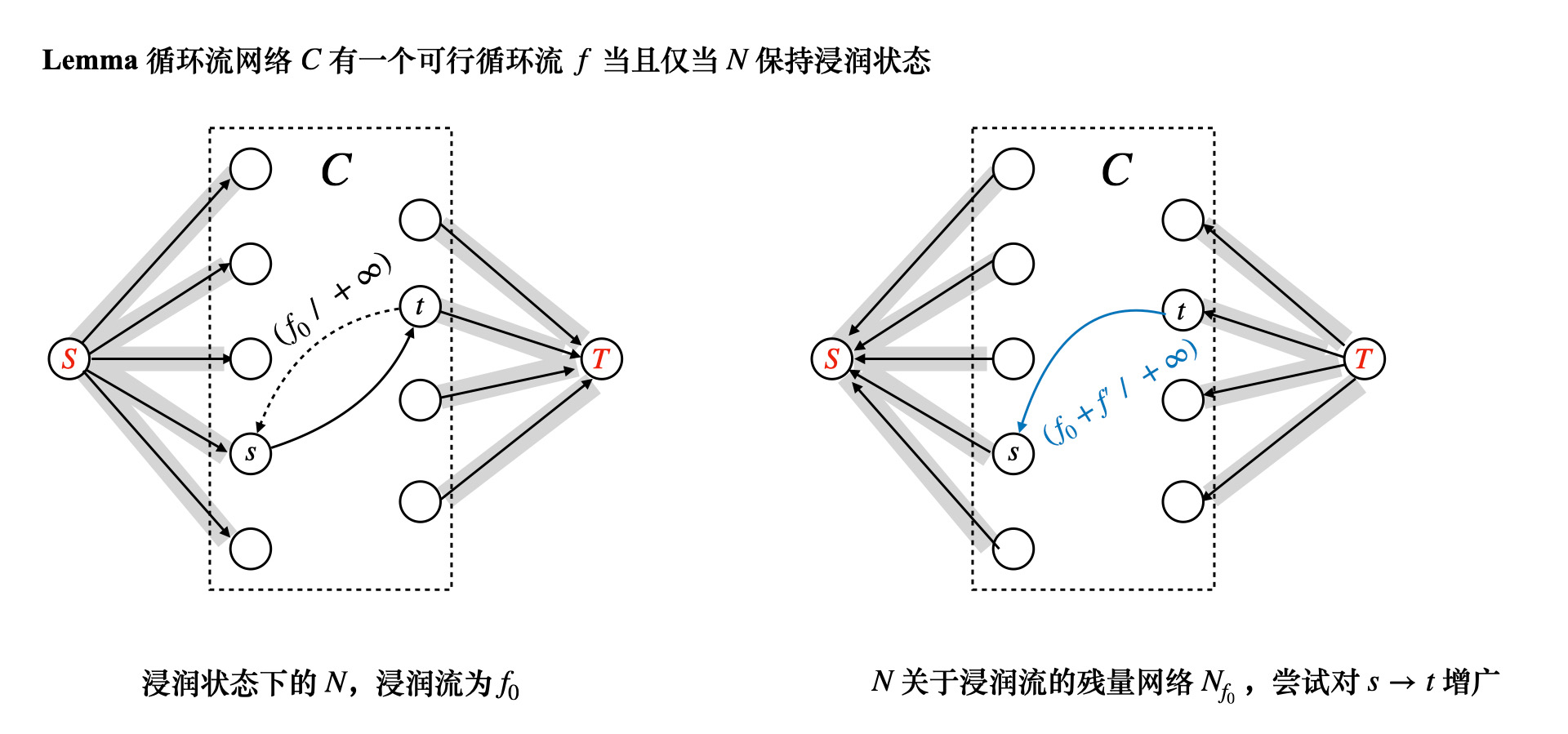
注意，这里对于浸润流 $f_0$，$f_0(s \to t)$ 的流量是分散的（因为 $s \to t$ 的路径上可能有很多点）
而 $f_0(t \to s)$ 是可以直接求的，因为我们在残量网络上连了一条 $t \to s, \ c(t, s) = +\infty$ 的边
因为 $f_0(s \to t) = f_0(t \to s) = c(s, t)$，所以求出 $f_0$ 之后
只需要在残量网络中找到表示 $\textbf{edge}(s, t)$ 这条边，即表示 $f_0(s \to t)$

const int maxn = 210, maxm = (10000 + maxn) * 2;
const int inf = 0x3f3f3f3f;

int head[maxn], ver[maxm], e[maxm], ne[maxm], idx = 1, tot = 0;
int A[maxn];
int n, m, s, t, S, T;
void add(int a, int b, int c) {
    ver[++idx] = b; e[idx] = c; ne[idx] = head[a]; head[a] = idx;
    ver[++idx] = a; e[idx] = 0; ne[idx] = head[b]; head[b] = idx;
}

int d[maxn], cur[maxn];
bool bfs() {
    memset(d, -1, sizeof d);
    queue<int> q;
    d[S] = 0, cur[S] = head[S];
    q.push(S);

    while (q.size()) {
        int x = q.front(); q.pop();
        for (int i = head[x]; i; i = ne[i]) {
            int y = ver[i];
            if (d[y] == -1 && e[i]) {
                d[y] = d[x] + 1;
                cur[y] = head[y];
                if (y == T) return true;
                q.push(y);
            }
        }
    }
    return false;
}

int dinic(int u, int lim) {
    if (u == T) return lim;
    int flow = 0;
    for (int i = cur[u]; i && lim > flow; i = ne[i]) {
        cur[u] = i;
        int v = ver[i];
        if (d[v] == d[u] + 1 && e[i]) {
            int t = dinic(v, min(e[i], lim - flow));
            if (!t) d[v] = -1;
            flow += t, e[i] -= t, e[i^1] += t;
        }
    }
    return flow;
}

int dinic() {
    int res = 0, flow;
    while (bfs()) while (flow = dinic(S, inf)) res += flow;
    return res;
}

int main() {
    freopen("input.txt", "r", stdin);
    scanf("%d%d%d%d", &n, &m, &s, &t);
    S = 0, T = n+1;

    for (int i = 0; i < m; i++) {
        int a, b, c, d;
        scanf("%d%d%d%d", &a, &b, &c, &d);
        add(a, b, d-c);
        A[a] -= c, A[b] += c;
    }
    for (int i = 1; i <= n; i++) {
        if (A[i] > 0) tot += A[i], add(S, i, A[i]);
        else if(A[i] < 0) add(i, T, -A[i]);
    }
    add(t, s, inf);

    // then solve
    if (dinic() != tot) {
        puts("No Solution");
        return 0;
    }

    int res = e[idx];
    e[idx] = e[idx-1] = 0;
    S = s, T = t;
    int ans = res + dinic();
    printf("%d\n", ans);
}