本文不对匈牙利算法的证明作解释。

预备知识

• 二分图： 设 $G=(V,E)$ 是一个无向图，如果顶点 $V$ 可分割为两个互不相交的子集 $(A,B)$ ，并且图中的每条边 $(i，j)$ 所关联的两个顶点 $i$ 和 $j$ 分别属于这两个不同的顶点集 $(i \in A,j \in B)$，则称图 $G$ 为一个二分图。
• 匹配：满足其中任意两条边都没有公共顶点的边集。
• 最大匹配：一个图所有匹配中，所含匹配边数最多的匹配，称为这个图的最大匹配。

简介

匈牙利算法用于求二分图的最大匹配。
模板题传送门： https://www.acwing.com/problem/content/description/863/

步骤

我们拿经典的男女配对来解释一下流程。

情境：给出 $n_1$ 个男生， $n_2$ 个女生，他们如果之间连边则代表着他们之间相互喜欢（不考虑同性恋（故保证是二分图））。

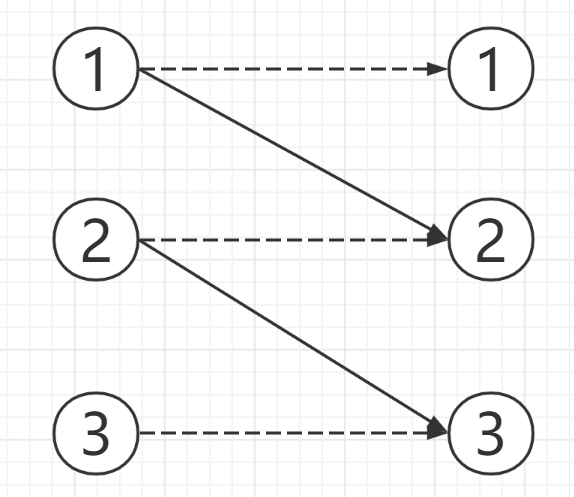
左边是男生，右边是女生。
一号男生和一、二号女生相互喜欢，二号男生和二、三号女生相互喜欢，三号男生和三号女生相互喜欢。

对于一号男生：
他和二号女生互相喜欢（假设他在找女友的时候优先遍历到二号女生），而二号女生现在没有男友，配对成功，返回。

对于二号男生：
他和三号女生互相喜欢（假设他在找女友的时候优先遍历到三号女生），而三号女生现在没有男友，配对成功，返回。

目前配对状况：

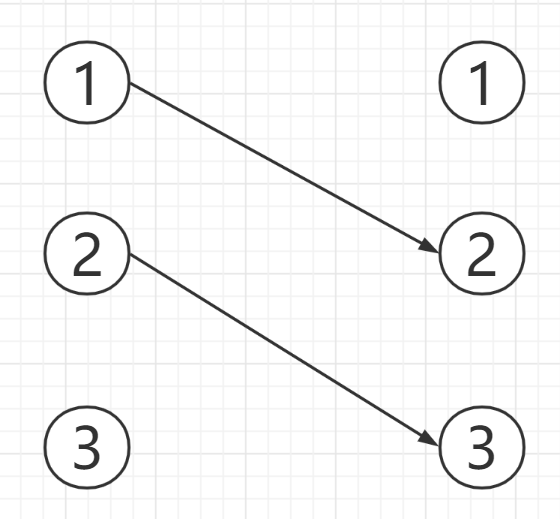
对于三号男生：
他和三号女生互相喜欢，但是此时三号女生有男友（二号）了，所以他标记了一下三号女生，然后去找到二号男生问他你能不能再去找一个其他女友（?），然后二号男生就去遍历他的女友，发现三号已经被标记了，但二号没有标记，但是此时二号女生有男友（一号）了，所以二号男生就标记了二号女生，类似于三号男生的行为，然后去找到一号男生问他你能不能再去找一个其他女友，一号男生也开始遍历自己的女友，最后发现一号女生没有标记，于是配对成功。

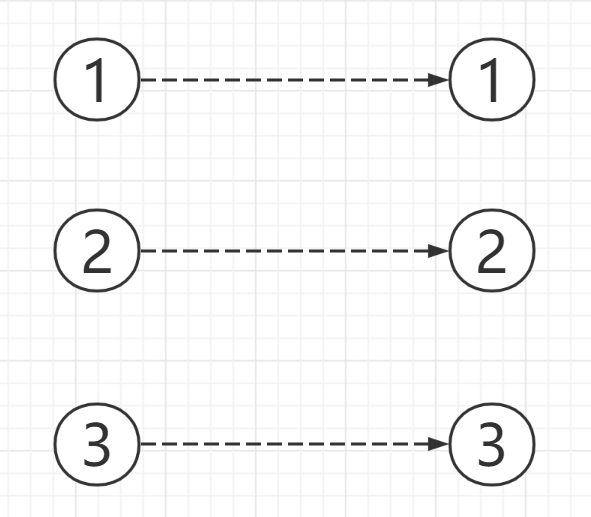
代码实现：
我们规定：

vis[i]=true 表示 i 号女生被标记，否则没有
match[i]=j 表示 i 号女生的男友是 j 号，如果没有男友则默认是 0

完整代码：

#include<bits/stdc++.h>
using namespace std;

const int N=505;
int n1,n2,m;

int h[N],tot;
struct node{
    int to,next;
}e[N*N];
void add(int u,int v){e[tot].to=v, e[tot].next=h[u], h[u]=tot++;}

int match[N];
bool vis[N];

bool find(int x){
    for(int i=h[x];~i;i=e[i].next){
        int go=e[i].to;
        if(!vis[go]){
            vis[go]=true;
            if(!match[go] || find(match[go])){
                match[go]=x;
                return true;
            }
        }
    }
    return false;
}

int main(){
    memset(h,-1,sizeof h);
    cin>>n1>>n2>>m;
    while(m--){
        int u,v; cin>>u>>v;
        add(u,v);
    }

    int res=0;
    for(int i=1;i<=n1;i++){
        memset(vis,false,sizeof vis);
        if(find(i)) res++;
    }
    cout<<res<<endl;

    return 0;
}