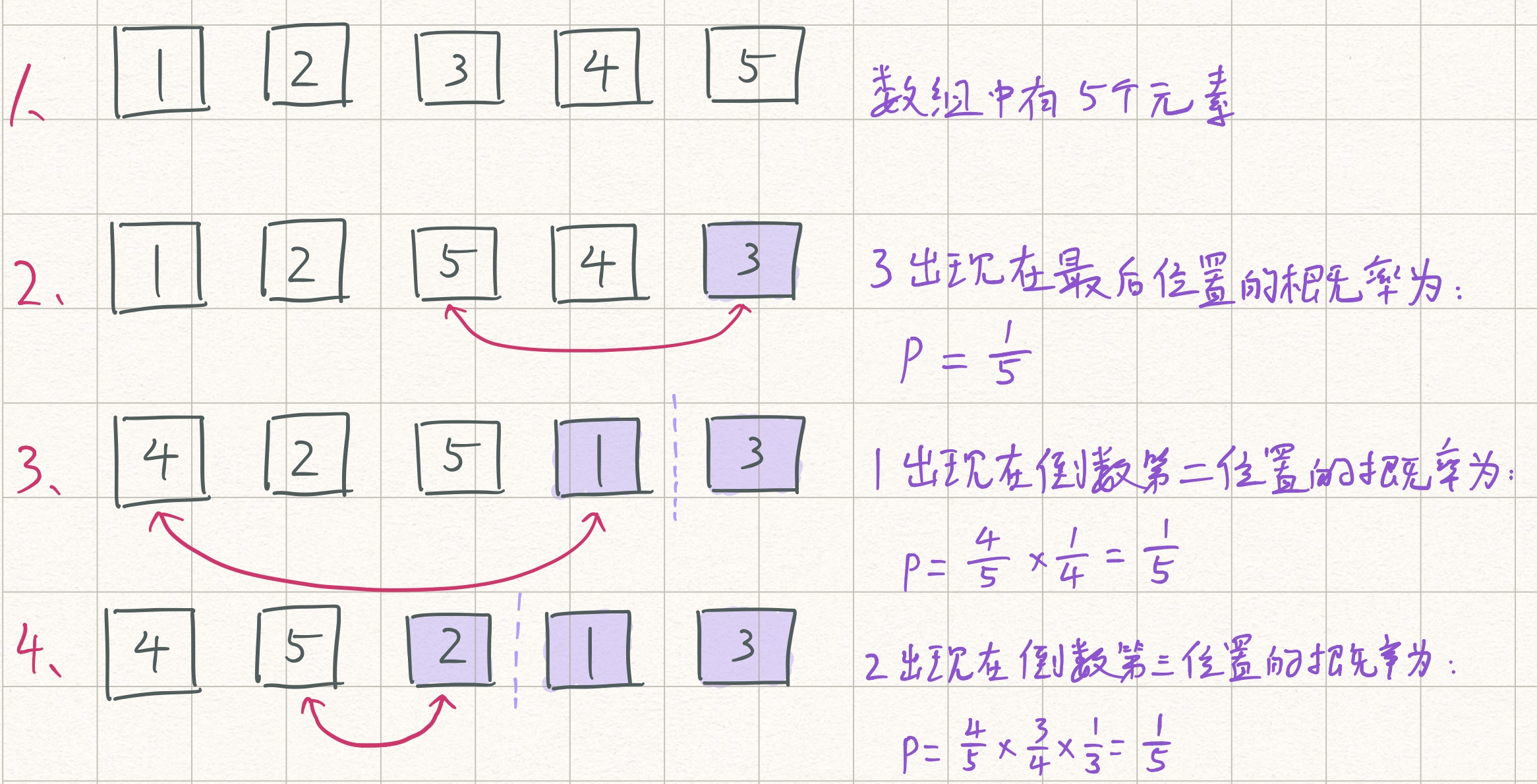
洗牌算法(Knuth shuffle算法):对于有n个元素的数组来说,为了保证洗牌的公平性,应该要能够等概率的洗出n!种结果。
举例解释如下:
- 开始数组中有五个元素;
- 在前五个数中随机选一个数与第五个数进行交换,每个数都有五分之一的概率被交换到最后一个位置;
- 在前四个数中随机选一个数与第四个数进行交换,每个数都有五分之一的概率被交换到第四个位置;
- 在前三个数中随机选一个数与第三个数进行交换,每个数都有五分之一的概率被交换到第三个位置;
综上所述,每个数都有相等的概率被放到任意一个位置中,即每个位置中出现任意一个数的概率都是相同的。这,就是洗牌算法。
时间复杂度:$O(N)$
class Solution {
private:
vector<int> original;
public:
Solution(vector<int>& nums) {
original = nums;
}
vector<int> reset() {
return original;
}
vector<int> shuffle() {
vector<int> nums(original); //用原数组来初始化新数组
for (int i = nums.size() - 1; ~i; i -- ) //从后往前遍历
{
swap(nums[i], nums[rand() % (i + 1)]); //rand()能随机生成0到最大随机数的任意整数
} //rand() % (i + 1)能随机生成0到i中的任意整数
return nums;
}
};
参考文献:
Knuth 洗牌算法

