代码

#include <algorithm>
#include <cstring>
#include <iostream>

using namespace std;

const int N = 1e5 + 10, M = 2 * N;

int n, m;

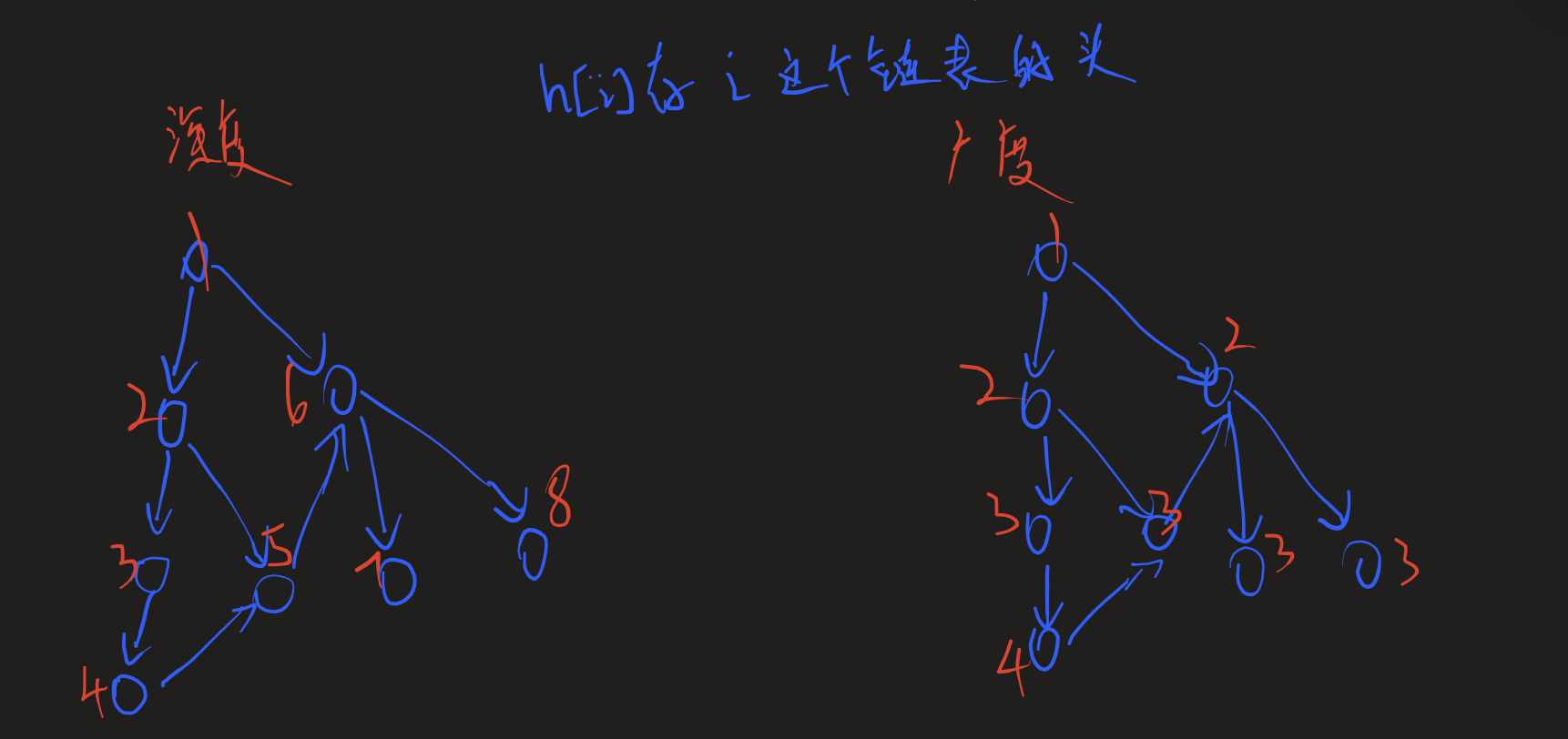
// head, e[M],ne[M],idx; 是一条单链表
// h[N], e[M],ne[M],idx; 是N条单链表
int h[N], e[M], ne[M], idx;

bool st[N];  // 用st数组存一下哪些点已经被遍历过了

int ans = N;  //记录一个全局最大值

// 在a对应的单链表中插入一个节点b
void add(int a, int b)
{
    e[idx] = b;         // 表示第idx条边指向b点
    ne[idx] = h[a];  // ne[idx]表示第idx条边的下一条边是 a点的邻接链表的第一条边
    h[a] = idx++;    // head[a]表示将a点的邻接链表的第一条边更新为第idx条边
}

// u表示当前已经dfs到的这个点
// 以u为根的子树中， 点的数量
int dfs(int u)
{
    st[u] = true;  // 标记一下， 当前这个点已经被搜索过

    int sum = 1;  // 记录当前子树大小
    int res = 0;  // 把u这个点删除之后， 每一个联通块的最大值

    for (int i = h[u]; i != -1; i = ne[i]) {
        int j = e[i];  // 当前这个链表中的节点， 对应图中的点的编号是多少
        if (!st[j]) {
            int s = dfs(j);     // j这棵子树的大小
            res = max(res, s);  //最大的联通块大小
            sum += s;
        }
    }
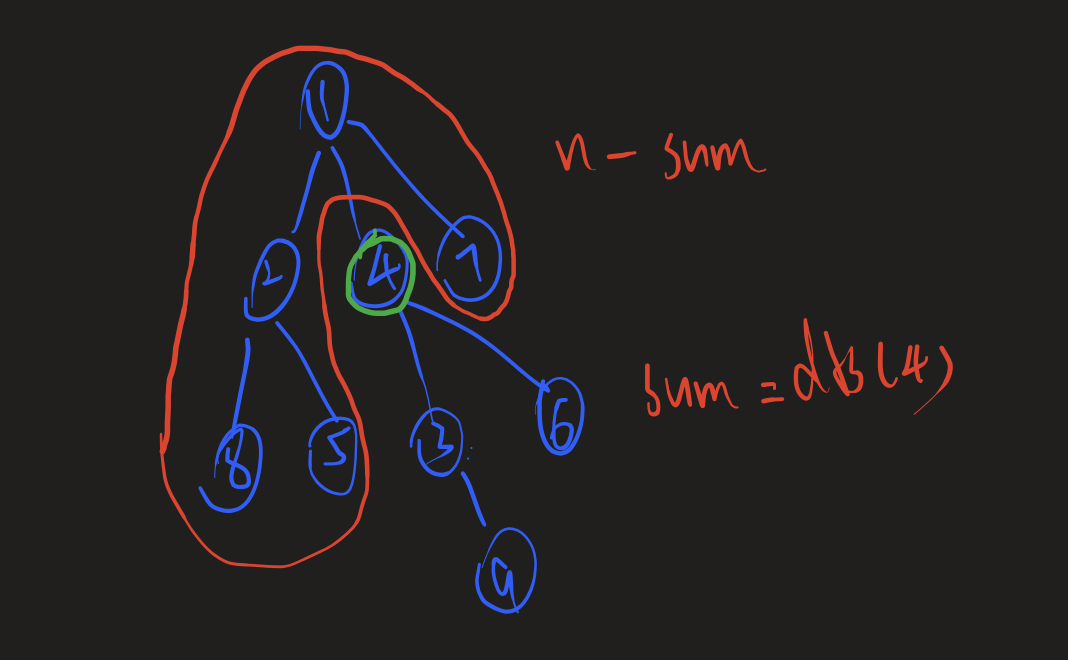
    res = max(res, n - sum);
    ans = min(ans, res);
    return sum;
}

int main()
{
    // 一条单链表 head初始化为-1
    // n条单链表，把所有的head初始化为-1
    memset(h, -1, sizeof h);

    cin >> n;
    for (int i = 0; i < n - 1; i++) {
        int a, b;
        cin >> a >> b;
        add(a, b);
        add(b, a);
    }

    // 随便挑一个点， 比方说从第一个点开始搜
    dfs(1);

    cout << ans << endl;

    return 0;
}