题目描述

给定一个由整数数组 A 表示的环形数组 C，求 C 的非空子数组的最大可能和。

在此处，环形数组意味着数组的末端将会与开头相连呈环状。（形式上，当0 <= i < A.length 时 C[i] = A[i]，且当 i >= 0 时 C[i+A.length] = C[i]）

此外，子数组最多只能包含固定缓冲区 A 中的每个元素一次。（形式上，对于子数组 C[i], C[i+1], …, C[j]，不存在 i <= k1, k2 <= j 其中 k1 % A.length = k2 % A.length）

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/maximum-sum-circular-subarray
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

样例

示例 1：

输入：[1,-2,3,-2]
输出：3
解释：从子数组 [3] 得到最大和 3
示例 2：

输入：[5,-3,5]
输出：10
解释：从子数组 [5,5] 得到最大和 5 + 5 = 10
示例 3：

输入：[3,-1,2,-1]
输出：4
解释：从子数组 [2,-1,3] 得到最大和 2 + (-1) + 3 = 4
示例 4：

输入：[3,-2,2,-3]
输出：3
解释：从子数组 [3] 和 [3,-2,2] 都可以得到最大和 3
示例 5：

输入：[-2,-3,-1]
输出：-1
解释：从子数组 [-1] 得到最大和 -1

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/maximum-sum-circular-subarray
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

(单调队列) $O(n)$

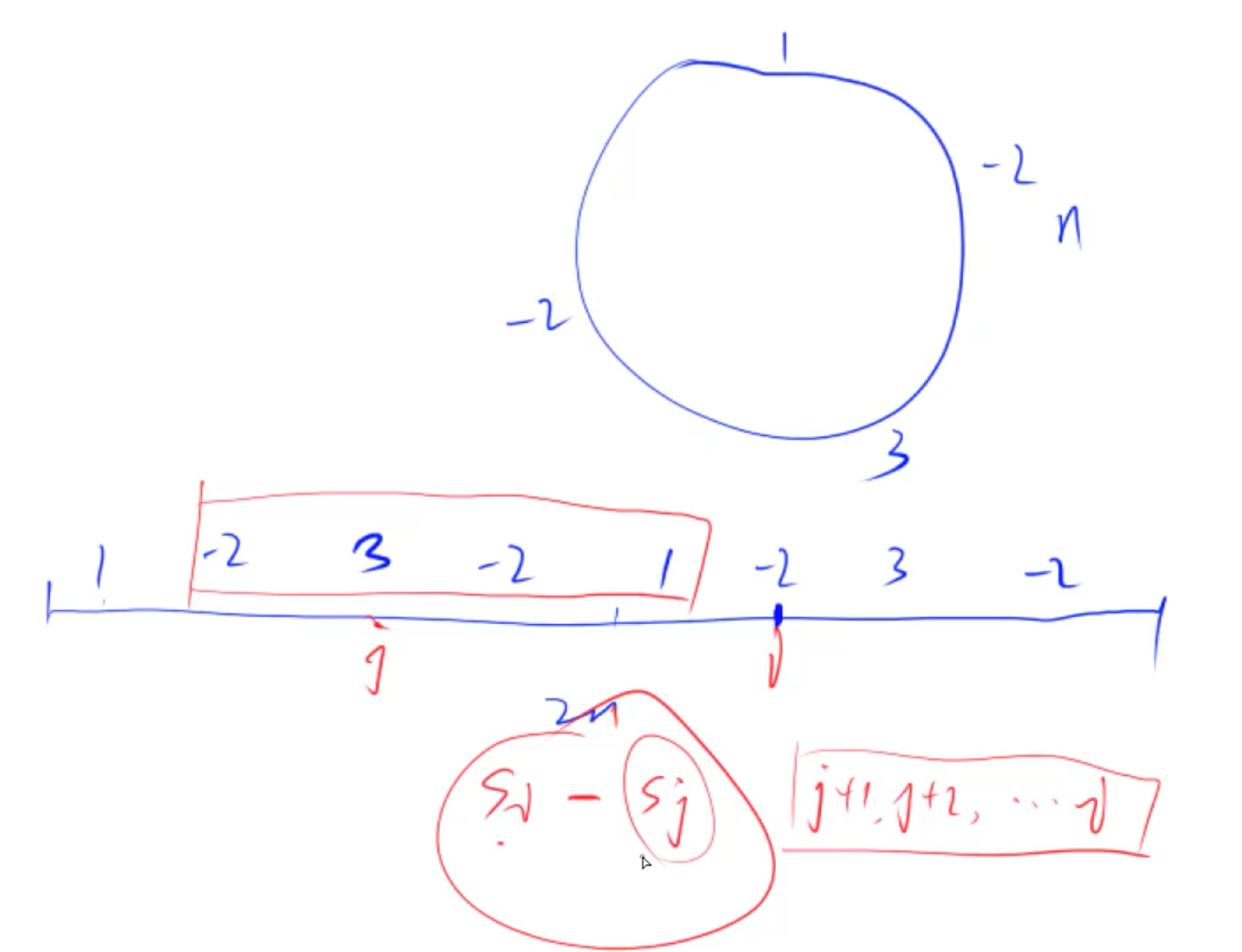
1 先将数组展开，复制一段加在后边；
2 求前缀和
3 维护一个单调递增队列
4 求最大子数组和，既是求 sum[i] - sum [j]最大，sum[i]固定，找到最小sum[j]即可（i j在n范围内）

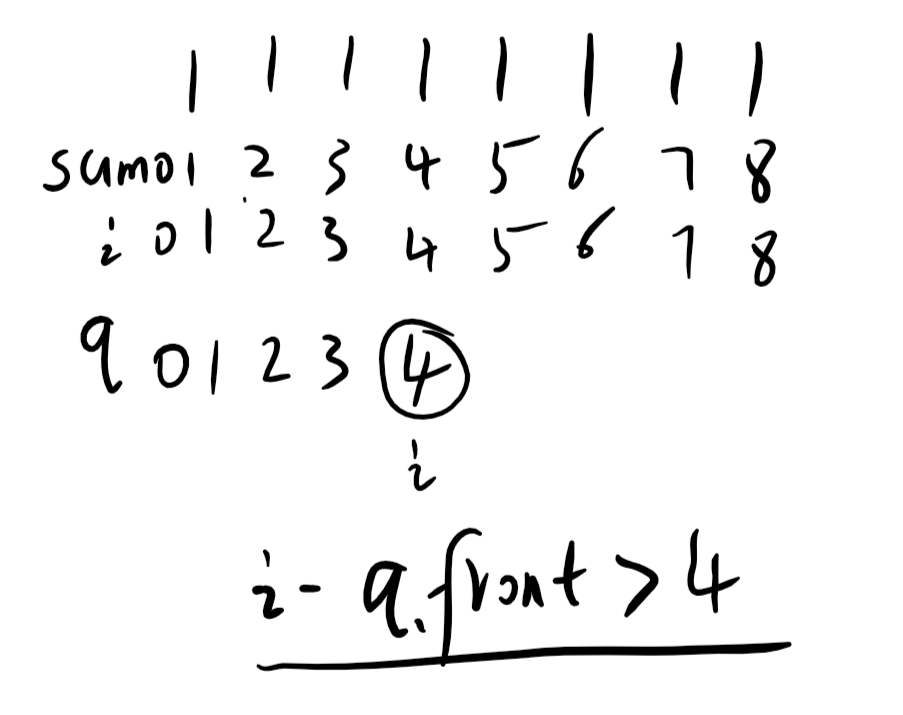
i-q.front()> n。如果 i-q.front()=n，会导致 q弹出pop一个元素，i 与新的队列头之间不是n个了

C++ 代码

class Solution {
public:
    int maxSubarraySumCircular(vector<int>& A) {
        int n=A.size();
        int res = INT_MIN;
        for(int i=0; i<n; ++i) A.push_back(A[i]);
        vector<int> sum(2*n+1,0);

        for(int i=1; i<2*n+1; ++i){
            sum[i] = sum[i-1] + A[i-1];
        }
        deque<int> q;
        q.push_back(0);

        for(int i=1; i<2*n+1; ++i){
            if(!q.empty() && i-n > q.front()) q.pop_front();//此时 i还未压入队列中，必须保证 sum[i]-sum[q.front()])的时候，队列包含n个数
            if(!q.empty()) res = max(res, sum[i]-sum[q.front()]);
            while(!q.empty() && sum[q.back()] >= sum[i]) q.pop_back();
            q.push_back(i);
        }
        return res;
    }
};