算法1

(数学) $O(n+q)$

首先我们令 $F(x) = f_N(\cdots(f_2(f_1(x))\cdots)$

当 $t_i = 1$ 时，图像向上移动

当 $t_i = 2$ 时，图像的最小值被限制在 $a_i$

当 $t_i = 3$ 时，图像的最大值被限制在 $a_i$

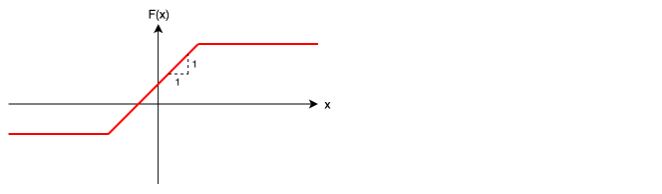
所以，我们可以通过 $f_i$ 的合成变成如下图像，即 存在 $a, l, r$ 使得 $F(x) = min(r, max(l, x + a))$

C++ 代码

#include <bits/stdc++.h>
#define rep(i, n) for (int i = 0; i < (n); ++i)

using std::cin;
using std::cout;
using std::max;
using std::min;
using ll = long long;

int main() {
    int n, q;
    cin >> n;

    ll s = 0;
    const ll INF = 1ll << 60;
    ll l = -INF, r = INF;
    rep(i, n) {
        ll a, t;
        cin >> a >> t;
        if (t == 1) { // +
            s += a;
            l += a;
            r += a;
        }
        else if (t == 2) { // max
            l = max(l, a);
            r = max(r, a);
        }
        else { // min
            l = min(l, a);
            r = min(r, a);
        }
    }

    cin >> q;
    rep(qi, q) {
        ll x;
        cin >> x;
        ll ans = x + s;
        if (ans < l) ans = l;
        if (ans > r) ans = r;
        cout << ans << '\n';
    }

    return 0;
}

算法2

(并查 集)

C++ 代码

#include<bits/stdc++.h>

using namespace std;
using int64 = long long;
// const int mod = 1e9 + 7;
const int mod = 998244353;

const int64 infll = (1LL << 62) - 1;
const int inf = (1 << 30) - 1;

struct IoSetup {
  IoSetup() {
    cin.tie(nullptr);
    ios::sync_with_stdio(false);
    cout << fixed << setprecision(10);
    cerr << fixed << setprecision(10);
  }
} iosetup;


template< typename T1, typename T2 >
ostream &operator<<(ostream &os, const pair< T1, T2 > &p) {
  os << p.first << " " << p.second;
  return os;
}

template< typename T1, typename T2 >
istream &operator>>(istream &is, pair< T1, T2 > &p) {
  is >> p.first >> p.second;
  return is;
}

template< typename T >
ostream &operator<<(ostream &os, const vector< T > &v) {
  for(int i = 0; i < (int) v.size(); i++) {
    os << v[i] << (i + 1 != v.size() ? " " : "");
  }
  return os;
}

template< typename T >
istream &operator>>(istream &is, vector< T > &v) {
  for(T &in : v) is >> in;
  return is;
}

template< typename T1, typename T2 >
inline bool chmax(T1 &a, T2 b) { return a < b && (a = b, true); }

template< typename T1, typename T2 >
inline bool chmin(T1 &a, T2 b) { return a > b && (a = b, true); }

template< typename T = int64 >
vector< T > make_v(size_t a) {
  return vector< T >(a);
}

template< typename T, typename... Ts >
auto make_v(size_t a, Ts... ts) {
  return vector< decltype(make_v< T >(ts...)) >(a, make_v< T >(ts...));
}

template< typename T, typename V >
typename enable_if< is_class< T >::value == 0 >::type fill_v(T &t, const V &v) {
  t = v;
}

template< typename T, typename V >
typename enable_if< is_class< T >::value != 0 >::type fill_v(T &t, const V &v) {
  for(auto &e : t) fill_v(e, v);
}

template< typename F >
struct FixPoint : F {
  FixPoint(F &&f) : F(forward< F >(f)) {}

  template< typename... Args >
  decltype(auto) operator()(Args &&... args) const {
    return F::operator()(*this, forward< Args >(args)...);
  }
};

template< typename F >
inline decltype(auto) MFP(F &&f) {
  return FixPoint< F >{forward< F >(f)};
}

/**
 * @brief Union-Find
 * @docs docs/union-find.md
 */
struct UnionFind {
  vector< int > data;

  UnionFind() = default;

  explicit UnionFind(size_t sz) : data(sz, -1) {}

  bool unite(int x, int y) {
    x = find(x), y = find(y);
    if(x == y) return false;
    if(data[x] > data[y]) swap(x, y);
    data[x] += data[y];
    data[y] = x;
    return true;
  }

  int find(int k) {
    if(data[k] < 0) return (k);
    return data[k] = find(data[k]);
  }

  int size(int k) {
    return -data[find(k)];
  }

  bool same(int x, int y) {
    return find(x) == find(y);
  }
};

int main() {
  int N, Q;
  cin >> N;
  vector< int64 > A(N);
  vector< int > T(N);
  for(int i = 0; i < N; i++) {
    cin >> A[i] >> T[i];
  }
  cin >> Q;
  deque< pair< int64, int > > qs;
  for(int i = 0; i < Q; i++) {
    int64 x;
    cin >> x;
    qs.emplace_back(x, i);
  }
  sort(begin(qs), end(qs));
  int64 padding = 0;
  UnionFind uf(Q);
  for(int i = 0; i < N; i++) {
    if(T[i] == 1) {
      padding += A[i];
    } else if(T[i] == 2) {
      int root = -1;
      while(qs.size() and max(A[i], qs.front().first + padding) == A[i]) {
        if(~root) uf.unite(root, qs.front().second);
        root = qs.front().second;
        qs.pop_front();
      }
      if(~root) {
        qs.emplace_front(A[i] - padding, root);
      }
    } else {
      int root = -1;
      while(qs.size() and min(A[i], qs.back().first + padding) == A[i]) {
        if(~root) uf.unite(root, qs.back().second);
        root = qs.back().second;
        qs.pop_back();
      }
      if(~root) {
        qs.emplace_back(A[i] - padding, root);
      }
    }
  }
  vector< int64 > ans(Q);
  for(auto &p : qs) {
    ans[uf.find(p.second)] = p.first + padding;
  }
  for(int i = 0; i < Q; i++) {
    cout << ans[uf.find(i)] << "\n";
  }
}