递归与分治—棋盘覆盖

题目描述

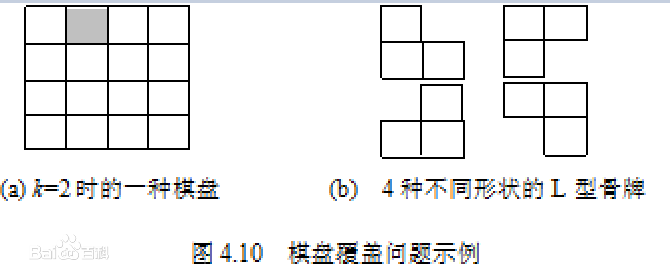
在一个 2^k * 2^k 个方格组成的棋盘中，若恰有一个方格与其它方格不同，则称该方格为一特殊方格，称该棋盘为一特殊棋盘。显然特殊方格在棋盘上出现的位置有 4^k 种情形。因而对任何 k>=0 ，有 4^k 种不同的特殊棋盘。下图所示的特殊棋盘为 k=2 时 16 个特殊棋盘中的一个。

在棋盘覆盖问题中，要用下图中 4 中不同形态的 L 型骨牌覆盖一个给定的特殊棋牌上除特殊方格以外的所有方格，且任何 2 个 L 型骨牌不得重叠覆盖。易知，在任何一个 2^k * 2^k 的棋盘中，用到的 L 型骨牌个数恰为 (4^k-1)/3 。现给出棋盘的大小和特殊方格所在的位置，请找出这种棋盘。

样例

4 1 1 

输出

3 3 4 4
3 1 2 4
5 2 2 6
5 5 6 6 

算法1

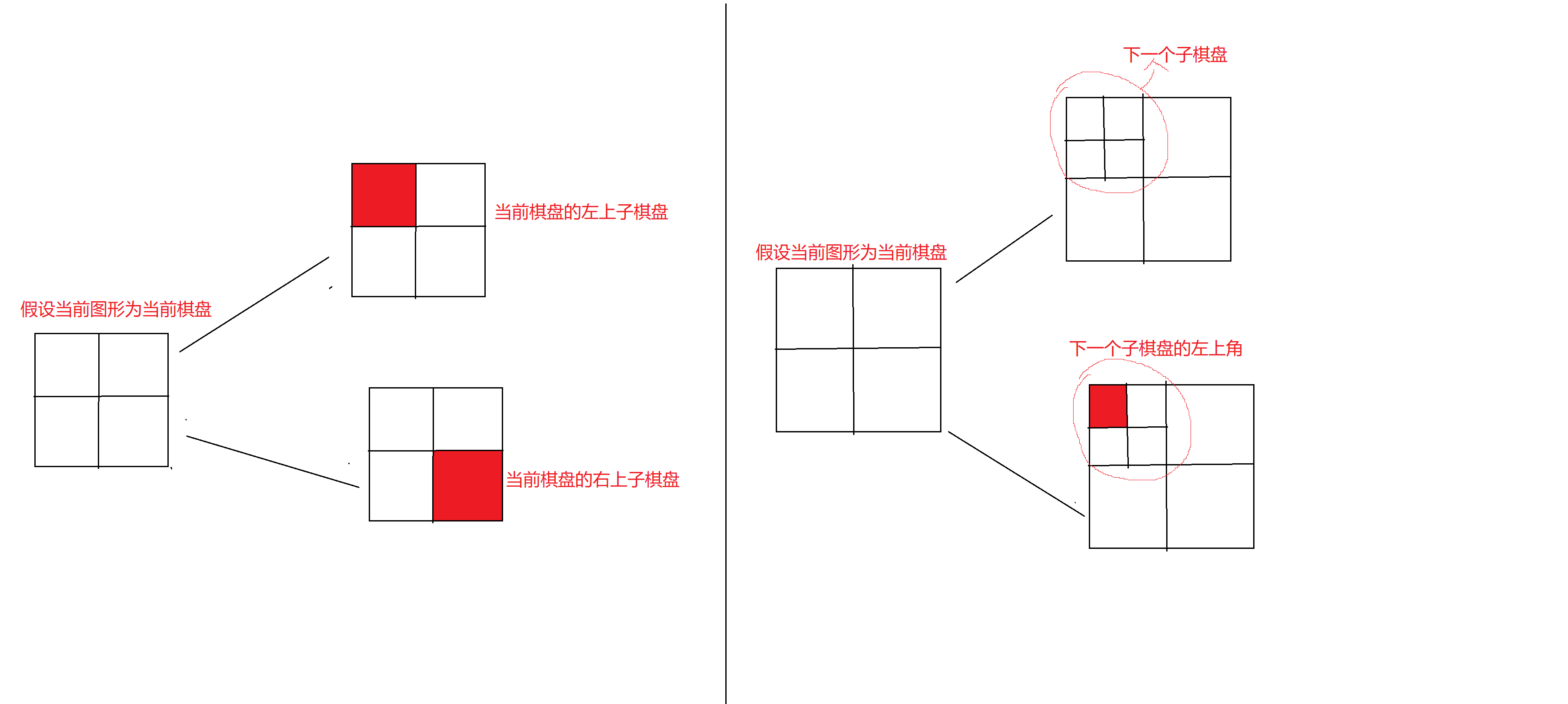
必定只有三个满足条件，所以形成不同形状的L图形

时间复杂度

(递归与分治) $O(4^k)$

C++ 代码

#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N = 110;
int chess[N][N];
int sized,x,y; //sized是棋盘的大小，x,y是特殊格的为止
int idx;  //表示当前L方格的编号,注意从2开始，1存初始只有一个的特殊格子


//stx,sty表示当前子棋盘的起点;X,y表示当前子棋盘的特殊格子，curs表示当前子棋盘的规模
void dfs(int stx,int sty,int x,int y,int curs){
    if(curs == 1) return;

    int t = ++idx;  //当前层的L方格编号
    int newcurs = curs / 2;
    //取4
    int cenx = stx + newcurs;
    int ceny = sty + newcurs;
    //判断当前特殊格子在不在左上子棋盘
    if(x < cenx && y < ceny){
        //如果在，则继续递归
        dfs(stx,sty,x,y,newcurs);  //下一次递归起点为下一个子棋盘的左上角坐标，特殊方格坐标照旧
    }else{
        //如果不在,则重新定一个特殊方格，为当前棋盘左上子棋盘的右下角,同时这个方块也是第idx个L的其中一个方格
        chess[cenx - 1][ceny - 1] = t;
        dfs(stx,sty,cenx - 1,ceny - 1,newcurs); //起点为下一个子棋盘的左上角坐标，特殊方格用新设置的那个
    }

    //判断特殊格子是否在右上子棋盘
    if(x < cenx && y >= ceny){
        dfs(stx,ceny,x,y,newcurs);  //起点为下一个子棋盘的左上角坐标，特殊方格坐标照旧
    }else{
        //将当前棋盘右上子棋盘的左下角设置为特殊方格
        chess[cenx - 1][ceny] = t;
        dfs(stx,ceny,cenx - 1,ceny,newcurs); //起点为下一个子棋盘的左上角坐标，特殊方格用新设置的那个
    }

    //判断特殊格子是否在左下子棋盘
    if(x >= cenx && y < ceny){
        dfs(cenx,sty,x,y,newcurs); //起点为下一个子棋盘的左上角坐标，特殊方格坐标照旧
    }else{
        //将当前棋盘左下子棋盘的右上角设置为特殊方格
        chess[cenx][ceny - 1] = t;
        dfs(cenx,sty,cenx,ceny - 1,newcurs); //起点为下一个子棋盘的右上角坐标，特殊方格用新设置的那个
    }

    //判断特殊格子是否在右下棋盘
    if(x>= cenx && y >= ceny){
        dfs(cenx,ceny,x,y,newcurs);  //起点为下一个子棋盘的左上角坐标，特殊方格坐标照旧
    }else{
        //当前棋盘右下子棋盘的左上角设置为特殊方格
        chess[cenx][ceny] = t;
        dfs(cenx,ceny,cenx,ceny,newcurs); //起点为下一个棋盘的左上角坐标，特殊方格坐标用新设置的那个
    }
}

int main(){
    cin >> sized;
    cin >> x >> y;
    chess[x][y] = idx = 1;
    dfs(0,0,x,y,sized);
    for(int i = 0;i < sized;++i){
        for(int j = 0;j < sized;++j){
            cout << chess[i][j] << ' ';
        }
        cout << endl;
    }
    return 0;
}