算法思路

维护一个集合S每次选择集合外边长最短的边并入集合中（集合外的边是指边两个顶点同时不在集合中），直到所有的点都在集合中,那么集合S中剩下的就是最小生成树了,我们来按照样例走一遍，先根据样例画出图

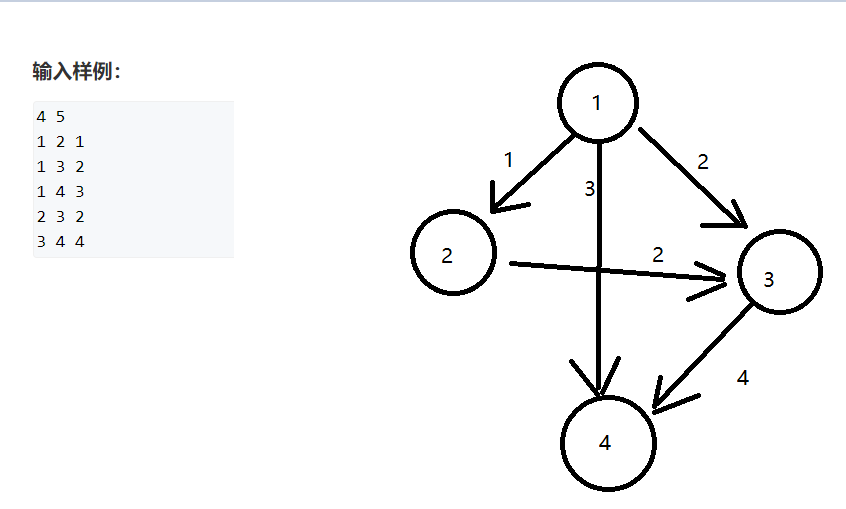
依次将集合S外边长最短的边加入集合S中，目前集合S为空，我们把边边长为1的边连同它的两个顶点并入集合S中

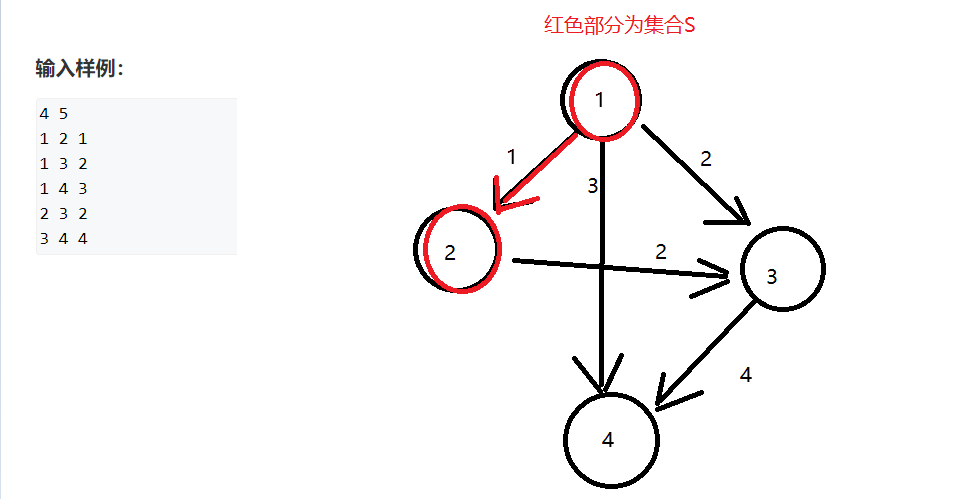
此时集合外最短的边的边长为2，有两条，我们任选一条并入集合S

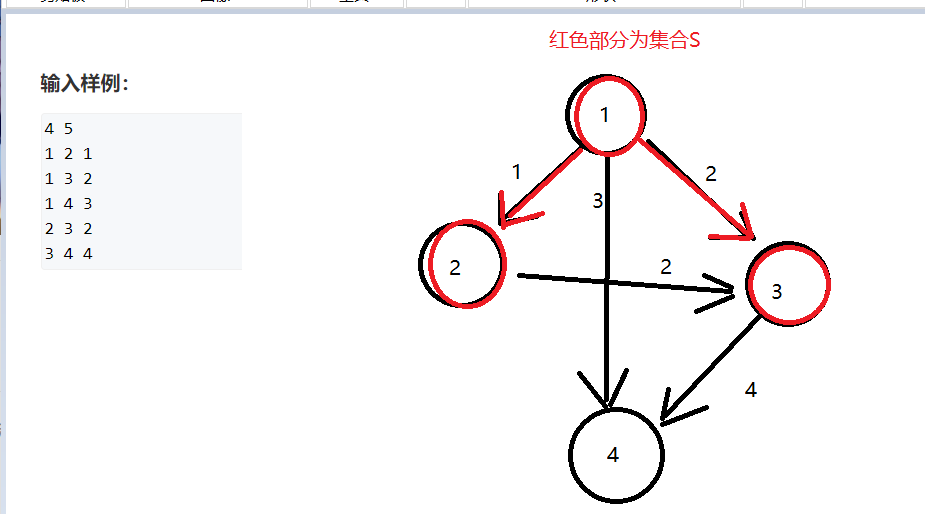
此时集合外最短的边为3，我们将它并入集合后，就没有位于集合外的点了，最小生成树构造完成

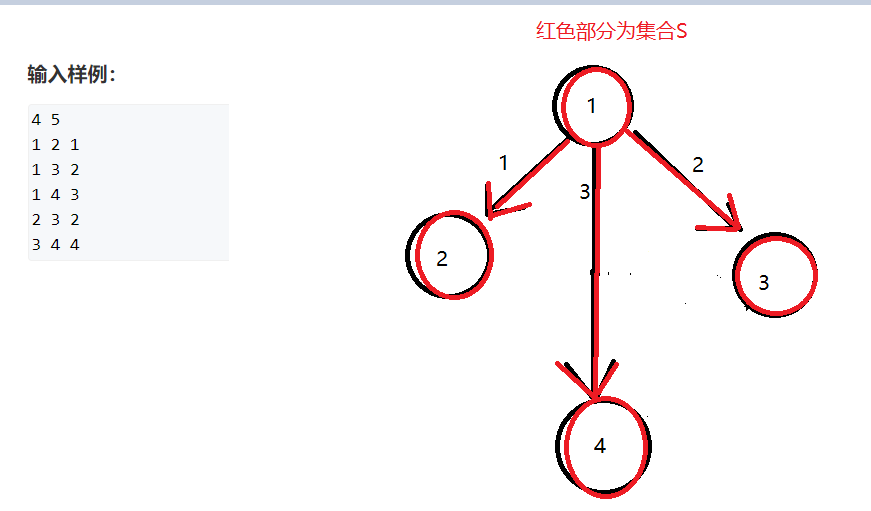
写代码

因为每次都是选择边长最短的边，因此我们可以先把边按权重排序
那我们就可以这样存储一条边

static public class Edge implements Comparable<Edge> {
        int a, b, w;

        /**
         * @param a //边的起点
         * @param b //边的终点
         * @param w //边的权重
         */
        public Edge(int a, int b, int w) {
            this.a = a;
            this.b = b;
            this.w = w;
        }

        @Override
        public int compareTo(Edge o) {
            // 比较器要求返回一个整数（正数代表o1>o2），我们想按照权重来排序，只需返回两者权重的差值即可
            return this.w - o.w;
        }
    }

其中compareTo方法是为了排序的时候对Edge类进行比较大小

Scanner scanner = new Scanner(System.in);

int n = scanner.nextInt(), m = scanner.nextInt();
int n = scanner.nextInt(), m = scanner.nextInt();
Edge[] g = new Edge[m];
// 读入所有边
for (int i = 0; i < m; i++) {
    int a = scanner.nextInt(), b = scanner.nextInt(), w = scanner.nextInt();
    g[i] = new Edge(a, b, w);
}
// 将所有边按权重排序
Arrays.sort(g);

存储的问题解决了之后我们要解决怎么判断一条边的两个顶点是否在同一个集合内的问题，
并查集可以快速的查询两个元素是否在同一个集合内，因此我们用并查集来解决
不会的并查集的同学看一下这个题： 并查集
核心问题解决了之后只需要从小到大遍历所有边，若此边的两个顶点不在同一个集合内，那么将此边加入到集合S中，同时更新此边的两个顶点到同一集合中，但是有的图它不存在最小生成树，由于一颗树n个顶点会有n-1条边，我们统计一下并入集合S中边的数量，若小于n-1那就是不存在最小生成树。

java代码

import java.util.Arrays;
import java.util.Scanner;

public class Main {

    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);

        int n = scanner.nextInt(), m = scanner.nextInt();
        Edge[] g = new Edge[m];
        int[] p = new int[n + 1]; // 并查集数组
        // 初始化并查集
        for (int i = 0; i <= n; i++)
            p[i] = i;
        // 读入所有边
        for (int i = 0; i < m; i++) {
            int a = scanner.nextInt(), b = scanner.nextInt(), w = scanner.nextInt();
            g[i] = new Edge(a, b, w);
        }
        // 将所有边按权重排序
        Arrays.sort(g);
        int res = 0, cnt = 0;
        for (int i = 0; i < m; i++) {
            int a = g[i].a, b = g[i].b;
            // 若a和b点不在同一个集合内
            int pa = find(a, p), pb = find(b, p);
            if (pa != pb) {
                // 将a和b合并
                p[pa] = pb;
                res += g[i].w;
                cnt++;
            }

        }
        // 一棵树n个顶点要n-1条边，少于n-1条说明无法构成最小生成树
        if (cnt < n - 1)
            System.out.println("impossible");
        else
            System.out.println(res);
        scanner.close();
    }

    // 并查集查询祖宗结点+路径压缩
    private static int find(int a, int[] p) {
        if (p[a] != a)
            p[a] = find(p[a], p);
        return p[a];
    }

    static public class Edge implements Comparable<Edge> {
        int a, b, w;

        /**
         * @param a //边的起点
         * @param b //边的终点
         * @param w //边的权重
         */
        public Edge(int a, int b, int w) {
            this.a = a;
            this.b = b;
            this.w = w;
        }

        @Override
        public int compareTo(Edge o) {
            // 比较器要求返回一个整数（正数代表o1>o2），我们想按照权重来排序，只需返回两者权重的差值即可
            return this.w - o.w;
        }
    }
}