问题描述

给定一个无向图 $G = (V, E)$，一个匹配是边的一个子集 $M \subseteq E$
使得对于所有节点 $\forall v \in V$，子集 $M$ 中最多有一条边与 $v$ 相连

对于节点 $v$，在子集 $M$ 中有边与 $v$ 相连，则称节点 $v$ 是由 $M$ 所匹配
否则，节点 $v$ 是没有匹配的
最大匹配 $M$，即对于任意匹配 $M’$，均有 $|M| \geqslant |M’|$

寻找最大二分匹配

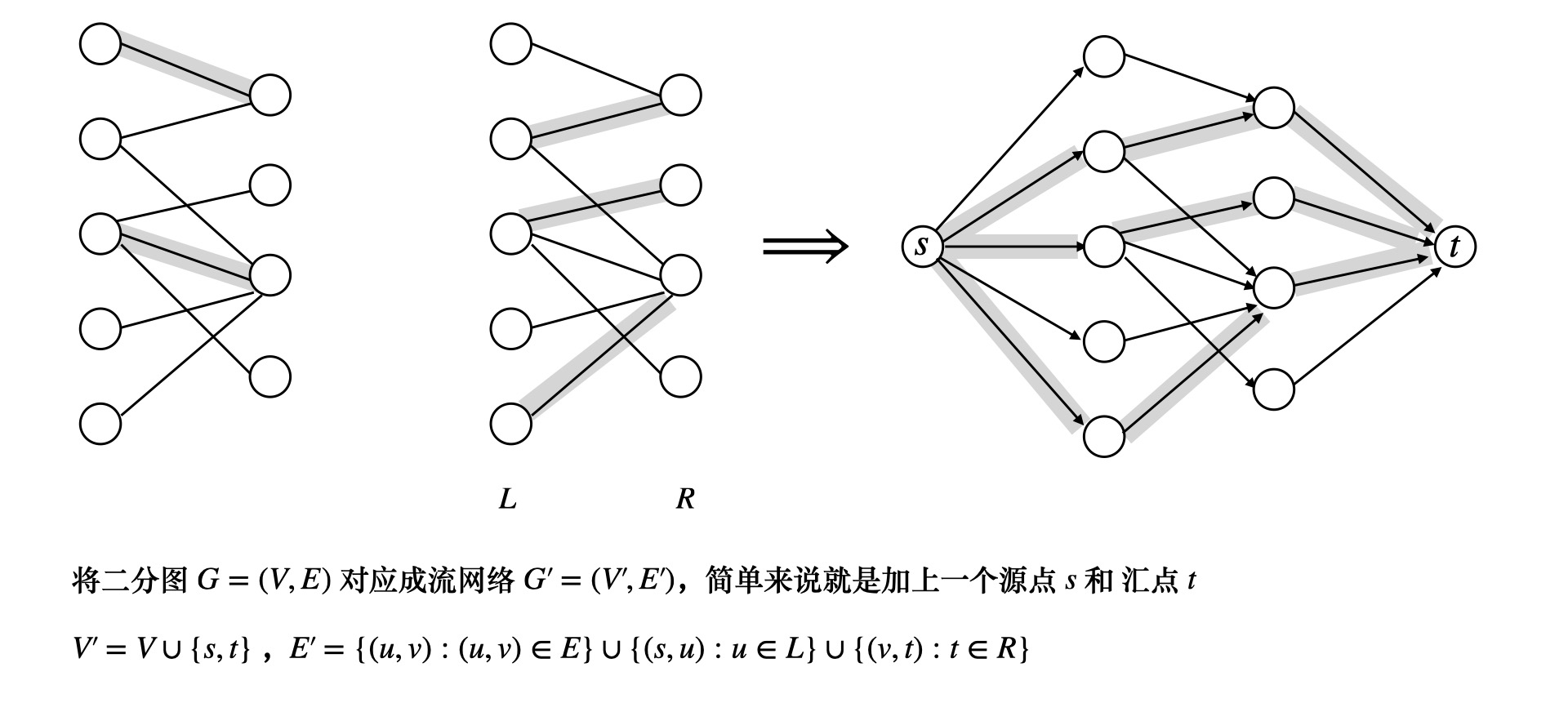
初步分析如下

• 每个节点至少有一条相连的边，所以 $|E| \geqslant |V|/2$
• $|E| \leqslant |E’| = |E| + |V| \leqslant 3|E|$

所以 $|E’| = \Theta (E)$

引理
设 $G = (V, E)$ 是一个二分图，其节点划分是 $V = L \cup R$，不妨设 $G’ = (V’, E’)$
是图 $G$ 对应的流网络。如果 $M$ 是 $G$ 中的一个匹配，则在流网络 $G’$ 中存在一个整数值的流 $f$
使得 $|f| = |M|$。相反，如果 $f$ 是 $G’$ 中的一个整数值的流，同样在 $G$ 中存在一个匹配 $M$，
使得 $|M|=|f|$

• 已知图 $G$ 的一个匹配 $M$，可以定义流 $f$ 如下

• 如果边 $(u, v) \in M \Longrightarrow f(s, u) = f(u, v) = f(v, t) = 1$
  而其他属于 $E’$ 的边 $(u, v)$，定义 $f(u, v) = 0$

• 另一方面，对于任意节点 $\forall \ v$，因为 $M$ 最多只有一条边与 $v$ 相连，
  所以子集 $M$ 中的边所诱导的路径 $s \to u \to v \to t$ 是节点不相交的
  横跨切割 $\{L \cup \{s\} , R \cup \{t\}\}$ 的净流量等于 $M$，$|M| = |f|$

• 设 $f$ 为 $G’$ 中的一个整数值的流，并且设
  $$ M = \{(u, v): u \in L, v \in R, \text{并且 } f(u, v) > 0\} $$

• 每个节点 $u \in L$ 仅有一条进入的边 $(s, u)$，容量为 $1$，也就是说最多有 $1$ 单位流量流入

• 根据流量守恒，离开节点的流也必须有 $1$ 个单位的流量，因为 $|f|$ 为整数，
  所以 $1$ 单位的流量只能最多从 $1$ 条边流出
  存在 $v \in R$，使得 $f(u, v) = 1$，并且 $u$ 的出边中仅有 $1$ 条带有正的权值
  由此，集合 $M$ 是一个匹配

• $\forall u \in L, f(s, u) = 1$，并且 $(u, v) \in E-M$，$f(u, v) = 0$
  横跨切割 $(L \cup \{s\}, R \cup \{t\})$ 的净流量 $f(L \cup \{s\}, R \cup \{t\}) = |M|$
  由此 $|M|=|f|$

推论
二分图 $G$ 中的一个最大匹配 $M$ 的基数等于其对应的流网络 $G’$ 中的某一最大流 $|f|$ 的值

如果 $M$ 是最大匹配，但 $|f|$ 不是最大流，那么存在一个最大流 $|f’| > |f|$
而根据引理，此时 $f’$ 对应原来二分图的一个匹配 $M’$，其基数为
$|M’| = |f’| > |f| = |M|$ 这与 $M$ 是一个最大匹配矛盾

同样，如果 $f$ 是 $G’$ 中的一个最大流，其对应的匹配是 $G$ 的一个最大匹配

• 方案输出，可以遍历所有的正向边

• 如果发现边的容量为 $0$，那么说明这个边被用到了，构成了一组方案

const int maxn = 100 + 10, maxm = 6000 + 10;
const int inf = 0x3f3f3f3f;
int head[maxn], ver[maxm], e[maxm], ne[maxm], tot = 1;
int n, m, S, T;

void add(int a, int b, int c) {
    ver[++tot] = b; e[tot] = c; ne[tot] = head[a]; head[a] = tot;
    ver[++tot] = a; e[tot] = 0; ne[tot] = head[b]; head[b] = tot;
}

int d[maxn], cur[maxn];
bool bfs() {
    memset(d, -1, sizeof d);
    queue<int> q;
    d[S] = 0, cur[S] = head[S];
    q.push(S);

    while (q.size()) {
        int x = q.front(); q.pop();
        for (int i = head[x]; i; i = ne[i]) {
            int y = ver[i];
            if (d[y] == -1 && e[i] > 0) {
                d[y] = d[x] + 1;
                cur[y] = head[y];
                if (y == T) return true;
                q.push(y);
            }
        }
    }
    return false;
}

int dinic(int u, int lim) {
    if (u == T) return lim;
    int flow = 0;
    for (int i = cur[u]; i && lim > flow; i = ne[i]) {
        cur[u] = i;
        int v = ver[i];
        if (d[v] == d[u] + 1 && e[i]) {
            int t = dinic(v, min(e[i], lim - flow));
            if (!t) d[v] = -1;
            flow += t, e[i] -= t, e[i^1] += t;
        }
    }
    return flow;
}

int dinic() {
    int res = 0, flow;
    while (bfs()) {
        while (true) {
            flow = dinic(S, inf);
            if (flow == 0) break;
            res += flow;
        }
    }
    return res;
}

int main() {
    freopen("input.txt", "r", stdin);
    scanf("%d%d", &m, &n);
    S = 0, T = n+1;
    for (int i = 1; i <= m; i++) add(S, i, 1);
    for (int i = m+1; i <= n; i++) add(i, T, 1);
    int a, b;
    while (scanf("%d%d", &a, &b) && a != -1) add(a, b, 1);

    // then solve
    printf("%d\n", dinic());
    for (int i = 2; i <= tot; i += 2) {
        if (ver[i] > m && ver[i] <= n && e[i] == 0) {
            printf("%d %d\n", ver[i^1], ver[i]);
        }
    }
}