题目描述

某国的军队由 N 个部门组成，为了提高安全性，部门之间建立了 M 条通路，每条通路只能单向传递信息，即一条从部门 a 到部门 b 的通路只能由 a 向 b 传递信息。

信息可以通过中转的方式进行传递，即如果 a 能将信息传递到 b，b 又能将信息传递到 c，则 a 能将信息传递到 c。

一条信息可能通过多次中转最终到达目的地。

由于保密工作做得很好，并不是所有部门之间都互相知道彼此的存在。

只有当两个部门之间可以直接或间接传递信息时，他们才彼此知道对方的存在。

部门之间不会把自己知道哪些部门告诉其他部门。

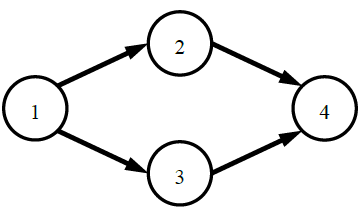
上图中给了一个 4 个部门的例子，图中的单向边表示通路。

部门 1 可以将消息发送给所有部门，部门 4 可以接收所有部门的消息，所以部门 1 和部门 4 知道所有其他部门的存在。

部门 2 和部门 3 之间没有任何方式可以发送消息，所以部门 2 和部门 3 互相不知道彼此的存在。

现在请问，有多少个部门知道所有 N 个部门的存在。

或者说，有多少个部门所知道的部门数量（包括自己）正好是 N。

输入格式

输入的第一行包含两个整数 N,M，分别表示部门的数量和单向通路的数量。所有部门从 1 到 N 标号。

接下来 M 行，每行两个整数 a,b，表示部门 a 到部门 b 有一条单向通路。

输出格式

输出一行，包含一个整数，表示答案。

输入样例

4 4
1 2
1 3
2 4
3 4

输出样例

2

样例解释

部门 1 和部门 4 知道所有其他部门的存在。

C++ 代码

#include<iostream>
#include<cstring>
#include<algorithm>

using namespace std;

const int N = 10010, M = 20010;

/*本代码使用数组来实现的有向图的邻接表*/

//存储每个顶点其中一条边的编号
int f1[N]; //正向存储图 （first1） 
int f2[N]; //反向存储图 （first2） 

int u1[M], v1[M];  //边的起点和终点(u——>v)
int u2[M], v2[M];  //边的起点和终点(u——>v)

int next1[M],next2[M];  //next[index]存储的是“编号为index的边”的“前一条边”的编号

bool st1[N];  //从顶点n出发，能到达的所有顶点的集合 
bool st2[N];  //从其它顶点出发，能到达顶点n的所有顶点的集合
int idx = 1;

void add(int first[], int a, int b, int u[], int v[], int next[])  //加边，头插法
{
    u[idx] = a;
    v[idx] = b;
    /*  next存储编号为index的边的前一条边的编号
        如果当前这条“编号为index的边”，是我们发现的以u[index]为起始顶点的第一条边，
        就将next[index]的值设为-1   */
    next[idx] = first[u[idx]];
    first[u[idx]] = idx;   //first存储顶点u[index]的其中一条边的编号
}

void dfs(int k, int f[], bool st[], int v[], int next[])
{
    st[k] = true; //当前结点（自己肯定知道自己），每遍历一个顶点就将其赋值为true 
    for(int i=f[k]; i != -1; i=next[i]) 
    {
        int j = v[i];
        if(!st[j])   //该顶点还没被遍历过 
        {
            dfs(j, f, st, v, next); 
        } 
    }
}

int main()
{
    int m,n;
    cin>>n>>m;
    memset(f1, -1, sizeof(f1));  //初始化first数组下标1~n的值为-1，表示1~n顶点暂时都没有边
    memset(f2, -1, sizeof(f2));
    while(m--)
    {
        int a, b;
        cin>>a>>b;
        add(f1, a, b, u1, v1, next1);
        add(f2, b, a, u2, v2, next2);
        idx++;
    }
    int res = 0;  //计数 
    for(int i=1; i<=n; i++)
    {
        memset(st1, 0, sizeof(st1));
        memset(st2, 0, sizeof(st2));
        dfs(i, f1, st1, v1, next1);
        dfs(i, f2, st2, v2, next2);
        int s = 0;
        for(int j=1; j<=n; j++)
        {
            if(st1[j] || st2[j])  //顶点i能到达顶点j，或者顶点j能到达顶点i 
            {
                s++;
            }
        }
        if(s == n)
        {
            res++;
        }
    }
    cout<<res<<endl;
    return 0;
}