状态压缩 状态转移

    解题思路 : 
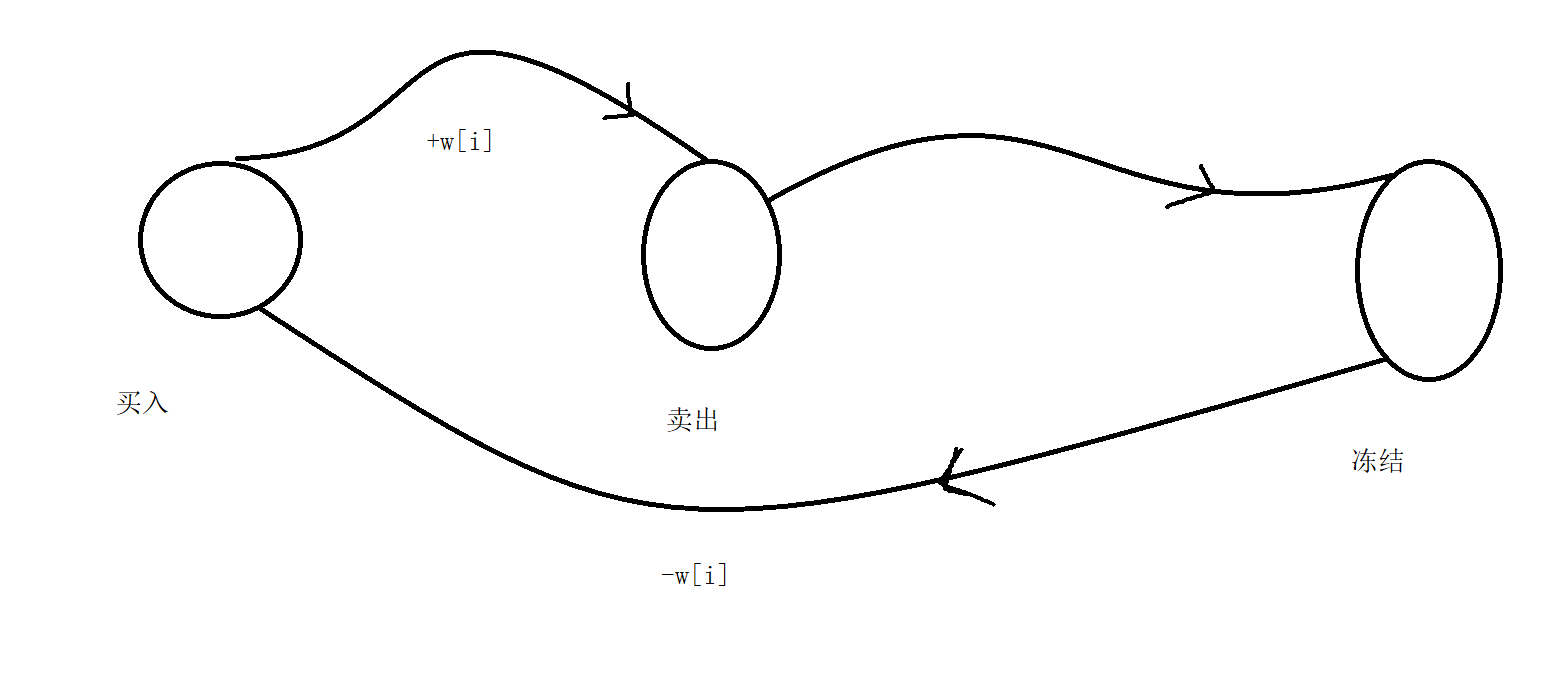
                1） 从上图可以看出f[0][2] - > f[0][0] - > f[0][1] 可以看出后两个状态是由前一个状态先后转移得到的所有应该不能直接被选择初始化未-INF
                ,f[0][2] = 0;
                2）考虑状态转移 : 第一个状态由 f[i - 1][2] - w[i] 得到
                                  第二个状态由 f[i - 1][0] + w[i] 得到
                                  第三个状态由 f[i-1][2] 或者 f[i - 1][1]得到

#include <iostream>
#include <algorithm>
#include <cstring>

using namespace std;
const int INF = 0x3f3f3f3f , N = 100010;
int n;
int f[N][3] , w[N];
int main() {


    cin >> n;
    for (int i = 1 ; i <= n ; i ++ ) cin >> w[i];
     f[0][0] = f[0][1] = -0x3f3f3f3f;
    f[0][2] = 0;
    for (int i = 1 ;  i <= n ; i ++ ) {
        f[i][0] = max(f[i - 1][2] - w[i] , f[i - 1][0]);
        f[i][1] = f[i - 1][0] + w[i];
        f[i][2] = max(f[i - 1][1] , f[i - 1][2]);
    }



    cout << max(f[n][1] , f[n][2]);
    return 0;
}

. 第二种解发

#include <queue>
#include <math.h>
#include <stack>
#include <stdio.h>
#include <iostream>
#include <string.h>
#include <algorithm>
using namespace std;
#define LL long long
const int N = 1e5 + 10;
int f[N];
int main()
{
    int n;
    cin >> n;
    int maxx = -0x3f3f;
    for(int i = 1,x,s ; i <= n ; i++)
    {
        cin >> x;
        maxx = i > 2 ? max(f[i-3] - s , maxx) : max(maxx, 0 - x); 
        f[i] = i > 1 ? max(f[i-1] , x + maxx) : f[i-1];
        s = x ;
    }
    cout << f[n] << endl;
}