状态压缩 状态转移

 解题思路 ：
            1) 首先我们从动态规划的本质开始考虑 ， 从前一个状态 通过做某种操作，到另一个状态的过程
            2) 从上述条件我们就可以来思考本题的状态转移了 : 
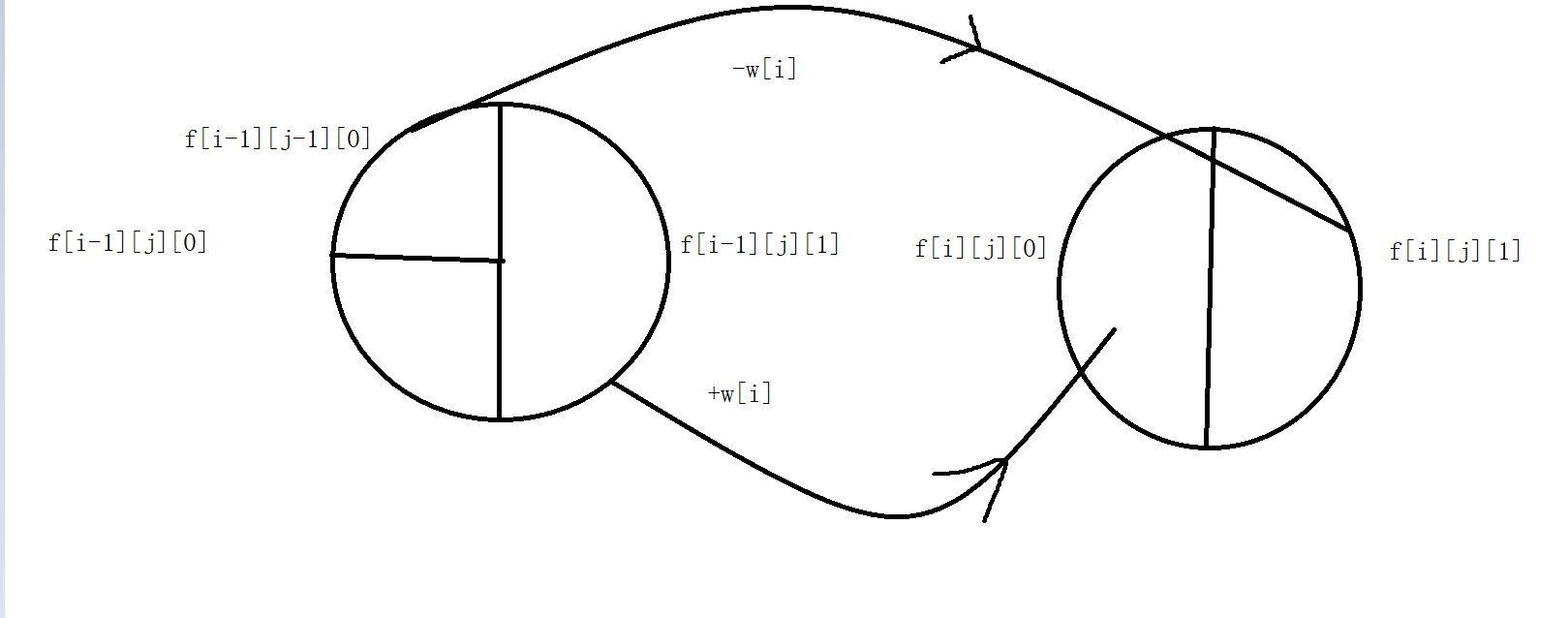
                2 - 1) 首先我们会用到的状态 f[i][j][0/1]  
                2 - 2) 上一层的状态 f[i - 1][j / j - 1][1 / 0] 
                        分析： 通过题意我们可以得知买入和卖出才能算一次买卖
                        ，所以我们买入f[i][j][1] 可以由f[i-1][j-1][0] + w[i] 得到 j - 1 的前一个状态根据 + w[i] 可以得到 f[j] ，具体可以参考0 / 1 背包问题
            3) 由于考虑到所有未使用的变量都不能使用我们把 f 初始化未 -INF , 对于每一种物品的f[1-n][0][0]表示没有开始选择所有 = 0;
            4）  f[i][j][1] = max(f[i - 1][j - 1][0] - w[i] , f[i - 1][j][1]);
                 f[i][j][0] = max(f[i - 1][j][1] + w[i] , f[i - 1][j][0]);   

代码

#include <iostream>
#include <algorithm>
#include <cstring>

using namespace std;
const int N = 100010 , M = 110;
int f[N][M][2] , w[N];
int n , m ;
int main() {

    cin >> n >> m;
    for (int i = 1 ; i <= n ;i ++ ) cin >> w[i];
    memset(f,0xcf,sizeof f);
    for (int i = 0 ; i <= n ; i ++ ) f[i][0][0] = 0;
    for (int i = 1 ; i <= n ; i ++ ) 
        for (int j = 1  ; j <= m ; j ++ ) {
            f[i][j][1] = max(f[i - 1][j - 1][0] - w[i] , f[i - 1][j][1]);
            f[i][j][0] = max(f[i - 1][j][1] + w[i] , f[i - 1][j][0]);
        }
    int res = 0; 
    for (int i = 1 ; i <= m ;i ++ ) res = max(res , f[n][i][0]);
    cout << res;
    return 0;
}

01 背包省略一维 万弘聚聚代码

#include<iostream>
#include<cstdio>
#include<cstring>
typedef long long ll;
#define MAXK 111
ll f[2][MAXK];
int main()
{
    ll n,k,x;
    scanf("%lld%lld",&n,&k);
    memset(f,0xcf,sizeof f);
    f[0][0]=0;
    for(ll i=1;i<=n;++i)
    {
        scanf("%lld",&x);
        for(ll j=k;j;--j)
        {
            f[0][j]=std::max(f[0][j],f[1][j]+x);
            f[1][j]=std::max(f[1][j],f[0][j-1]-x);
        }
    }
    ll ans=0;
    for(ll i=0;i<=k;++i)ans=std::max(ans,std::max(f[0][i],f[1][i]));
    printf("%lld",ans);
    return 0;
}

作者：whsstory
链接：https://www.acwing.com/solution/content/5055/
来源：AcWing
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。