算法2

Bellman-Ford算法

时间复杂度 O(nm)O(nm), nn 表示点数，mm 表示边数
注意在模板题中需要对下面的模板稍作修改，加上备份数组，详情见模板题。

int n, m;       // n表示点数，m表示边数
int dist[N];        // dist[x]存储1到x的最短路距离

struct Edge     // 边，a表示出点，b表示入点，w表示边的权重
{
    int a, b, w;
}edges[M];

// 求1到n的最短路距离，如果无法从1走到n，则返回-1。
int bellman_ford()
{
    memset(dist, 0x3f, sizeof dist);
    dist[1] = 0;

    // 如果第n次迭代仍然会松弛三角不等式，就说明存在一条长度是n+1的最短路径，由抽屉原理，路径中至少存在两个相同的点，说明图中存在负权回路。
    for (int i = 0; i < n; i ++ )
    {
        for (int j = 0; j < m; j ++ )
        {
            int a = edges[j].a, b = edges[j].b, w = edges[j].w;
            if (dist[b] > dist[a] + w)
                dist[b] = dist[a] + w;
        }
    }

    if (dist[n] > 0x3f3f3f3f / 2) return -1;
    return dist[n];
}

思路

所用的数据结构
dist[N]表示从起点到当前点的当前最短距离

backup[j]表示每次进入第2重循环的dist数组的备份

算法步骤
0.初始化dist数组为正无穷，dist[1]=0;

1.（外重循环）循环i从1到n，遍历n次指的：是不经过i条边到达终点的最短距离

经过n次操作n个点的最短距离也就确定了；

2.（内重循环）循环j从1到m，遍历m条边，把所有边都进行松弛操作；

每次取出两点以及他们连接的边的权重（a,b,w表示a—>b的一条边）；

用从起点到a的当前最短距离+权重来更新从起点到b的当前最短距离；
dist[b]=min(dist[b],dist[a]+w);

3.返回答案；

为什么跑完算法就能算出最短距离呢
因为第二重循环遍历了m条边，每条都被遍历了n次；

所以这n个点的所有他的前驱后继相对应的边权一定都被遍历到了

又因为他是有松弛操作的，所以只要上一个点（前驱）的当前最短路求出来了

这个点就可以用他的前驱来更新他的最短距离，从而他的后继又可以用它来更新最短距离了

backup干啥使的
backup[j]表示每次进入第2重循环的dist数组的备份。
如果不加这个备份的话有可能会发生节点最短距离的串连；
比如说：
图1
现在从3号结点走到4号节点要想进行松弛操作就必须先得到dist[3]，要想得到dist[3]就得知道dist[2]；
dist[2]=2，现在dist[3]是正无穷，用2号结点来更新3号结点，dist[3]=2+3=5;

现在要更新dist[4]了，此时dist[4]=正无穷

出现问题了，dist[4]是用dist[3]是用正无穷来更新还是5呢

用dist[3]=5来更新那是下一次i迭代的事情；
这道题说是不经过k条边，说不定下一次就到k条边了，所以还是得用正无穷来更新的

第3步的细节
怎么返回呢还是这样吗？

if(dist[n]==0x3f3f3f3f)return -1;
else return dist[n];
比如说这样：
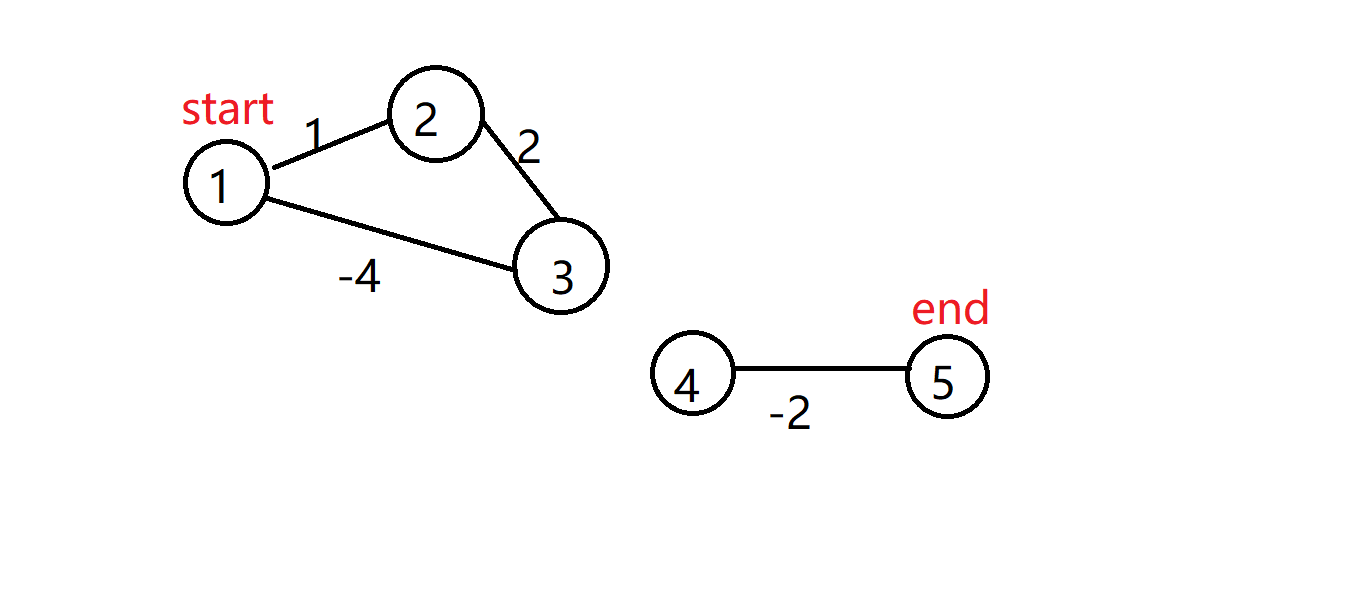
图2
这个奇葩起点和终点居然不连通

3号点在经过松弛操作后可能会更新4号点，因为正无穷-2<正无穷吗；

所以终点就不是正无穷了，所以就返回正无穷-2了，不对

又因为如果正无穷减也不会减的太大（数据保证边权的绝对值不大于100000）

所以就直接这样写

if(dist[n]>=0x3f3f3f3f/2)return -1;
else return dist[n];
时间复杂度 O(nm);

图1

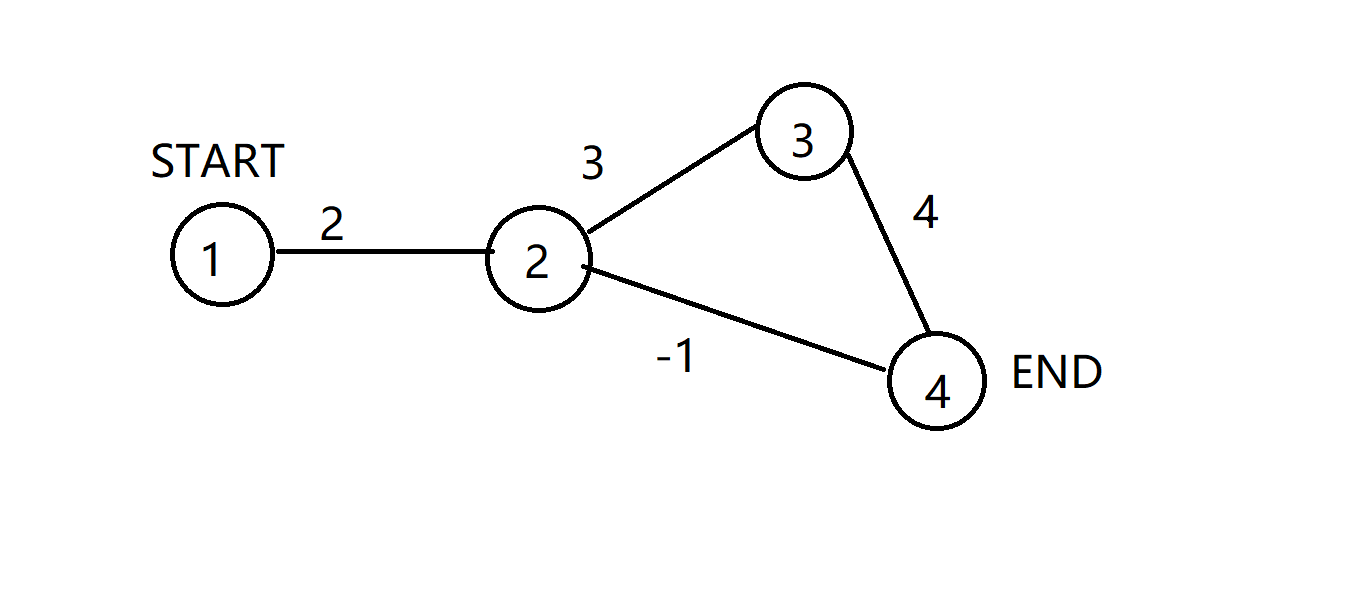
图2

C++ 代码

#include<bits/stdc++.h>
using namespace std;
const int N=100010;
int dist[N],backup[N];
int k,n,m;
struct edge{
    int a;int b;int w;
}edge[N];
int bellman_ford()
{
    memset(dist,0x3f,sizeof dist);
    dist[1]=0;
    for(int i=1;i<=k;i++)
    {
        memcpy(backup,dist,sizeof dist);
        for(int j=1;j<=m;j++)
        {
            int a=edge[j].a,b=edge[j].b,w=edge[j].w;
            dist[b]=min(dist[b],backup[a]+w);
        }
    }
    if(dist[n]>=0x3f3f3f3f/2)return -1;
    else return dist[n];
}
int main()
{
    cin>>n>>m>>k;
    for(int i=1;i<=m;i++)
    {
        int a,b,c;
        cin>>a>>b>>c;
        edge[i].a=a,edge[i].b=b,edge[i].w=c;
    }
    int t=bellman_ford();
    if(t==-1)puts("impossible");
    else cout<<t<<endl;
}