AcWing 2171. EK求最大流

历史记录

清除记录

猜你想搜

AcWing热点
App
登录/注册

AcWing 2171. EK求最大流原题链接中等

作者：

心里没有一点AC数 , 2021-03-16 21:03:04 , 所有人可见 , 阅读 1954

53

33

说明
在网络流相关问题中，在流网络（原网络） $G=(V, E)$ 中不考虑反向边
只有在任意流 $\forall f$ 所对应的残量网络 $G_f$ 中，才考虑反向边

流网络

一个源点 $s$ 和一个汇点 $t$
边集合 $E$ 中包含一条边 $(u, v)$，则不存在反向边 $(v, u)$
边的容量值为 $c(u, v)$，流量为 $f(u, v)$

容量限制
$$ \forall u, v \in V, \quad 0 \leqslant f(u, v) \leqslant c(u, v) $$
流量守恒
$$ \forall u \in V - \{s, t\}, \quad \sum_{v \in V} f(v, u) = \sum_{v \in V} f(u, v) $$
特别地，如果 $(u, v) \notin E, f(u, v) = 0$
流的定义
$$ |f| = \sum_{v \in V} f(s, v) - \sum_{v \in V} f(v, s) $$

Ford-Fulkerson 方法

初始化流为 $f = 0$
$\textbf{while}$ $\text{在残量网络 } G_f \ \text{中存在一条增广路径} \ p$
$\text{沿着} \ p \ \text{增加流} \ f$
$\textbf{return} \ f$

残量网络

$$ c_f(u, v) = \begin{cases} c(u, v) - f(u, v) && \text{如果} \ (u, v) \in E \\\ f(v, u) && \text{如果} \ (v, u) \in E \\\ 0 && \text{其他} \end{cases} $$

$f’$ 为残量网络中的一个流，定义 $f’ \uparrow f$ 为流 $f’$ 对 $f$ 的递增
$$ (f \uparrow f’)(u, v) = \begin{cases} f(u, v) + f’(u, v) - f’(v, u) && \text{若} (u, v) \in E \\\ 0 && \text{其他} \end{cases} $$

引理1
$G(V, E)$ 为流网络，设 $f$ 为 $G$ 中的一个流，$G_f$ 为对应的残量网络
$f’$ 为 $G_f$ 中的一个流，那么 $f \uparrow f’$ 为 $G$ 中的一个流
并且 $|f \uparrow f’| = |f| + |f’|$
容量限制，$f’(v, u) \leqslant c_f(v, u) = f(u, v)$
$$ \begin{aligned} (f \uparrow f’)(u, v) &= f(u, v) + f’(u, v) - f’(v, u) \xrightarrow{f’(v,u) \leqslant f(u,v)} \\\ &\geqslant f(u, v) + f’(u, v) - f(u, v) = f’(u, v) \geqslant 0 \end{aligned} $$
$$ \begin{aligned} (f \uparrow f’)(u, v) &= f(u, v) + f’(u, v) - f’(v, u) \xrightarrow{f’(v,u) \geqslant 0} \\\ &\leqslant f(u, v) + f’(u, v) \leqslant f(u, v) + c_f(u, v) \\\ &= f(u, v) + c(u, v) - f(u, v) = c(u, v) \end{aligned} $$
流量守恒，对于所有节点 $u \in V - \{s, t\}$
$$ \begin{aligned} \sum_{v \in V}(f \uparrow f’)(u, v) &= \sum_{v \in V} \left( f(u, v) + f’(u, v) - f’(v, u) \right) \\\ &= \sum_{v \in V} f(u, v) + \sum_{v \in V} f’(u, v) - \sum_{v \in V} f’(v, u) \xrightarrow{\text{流量守恒}} \\\ &= \sum_{v \in V} f(u, v) + \sum_{v \in V} f’(v, u) - \sum_{v \in V} f’(u, v) \\\ &= \sum_{v \in V} \left( f(v, u) + f’(v, u) - f’(u, v) \right) \\\ &= \sum_{v \in V} (f \uparrow f’)(v, u) \end{aligned} $$
流量计算
$V_1 = \{v : (s, v) \in E\}$ 表示从源点 $s$ 流出的流量，流量能到达的点的集合
$V_2 = \{v : (v, s) \in E\}$ 表示流回源点 $s$ 的流量，这些流量经过的点集
$$ |f \uparrow f’| = \sum_{v \in V_1} (f \uparrow f’)(s, v) - \sum_{v \in V_2} (f \uparrow f’)(v, s) $$
$$ \begin{aligned} |f \uparrow f’| &= \sum_{v \in V_1} (f(s, v) + f’(s, v) - f’(v,s)) - \sum_{v\in V_2}(f(v,s) + f’(v,s) - f’(s, v)) \\\ &= \sum_{v \in V_1}f(s, v) + \sum_{v \in V_1}f’(s, v) - \sum_{v \in V_1}f’(v, s) \\\ &\quad - \sum_{v \in V_2}f(v, s) - \sum_{v \in V_2}f’(v,s) + \sum_{v \in V_2} f’(s, v) \\\ &= \sum_{v \in V_1} f(s, v) - \sum_{v \in V_2}f(v,s) \\\ &\quad + \left(\sum_{v \in V_1}f’(s, v) + \sum_{v \in V_2}f’(s, v) \right) - \left(\sum_{v \in V_1}f’(v, s) + \sum_{v \in V_2}f’(v,s) \right) \\\ &= \left( \sum_{v \in V_1}f(s, v) - \sum_{v \in V_2}f(v,s) \right) + \left( \sum_{v \in V_1 \cup V_2} f’(s, v) - \sum_{v \in V_1 \cup V_2} f’(v,s) \right) \end{aligned} $$
$$ |f \uparrow f’| = |f| + |f’| $$

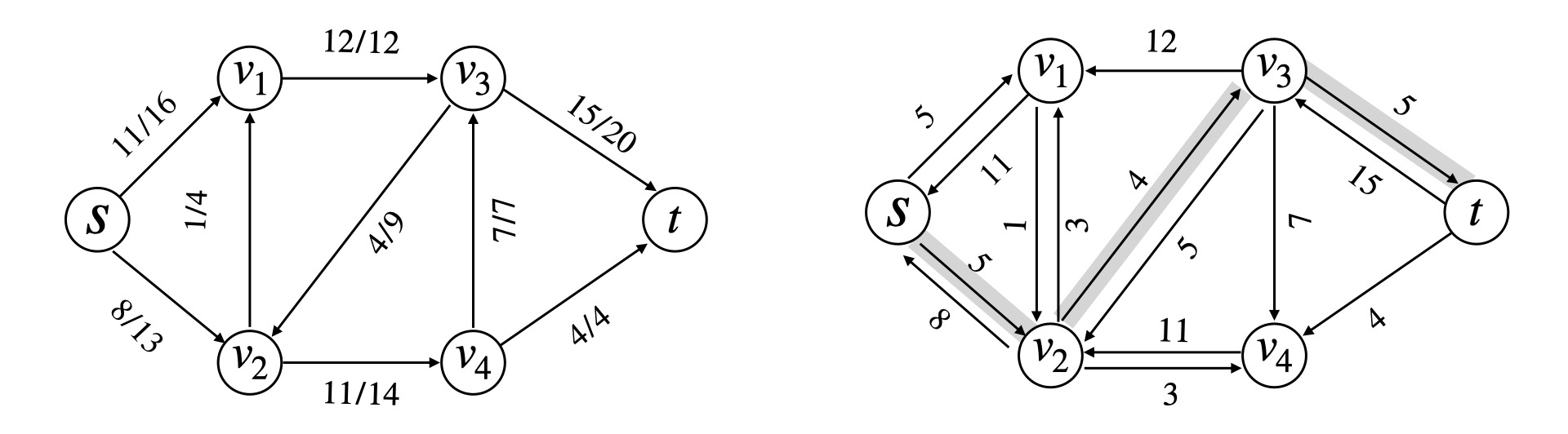
增广路径

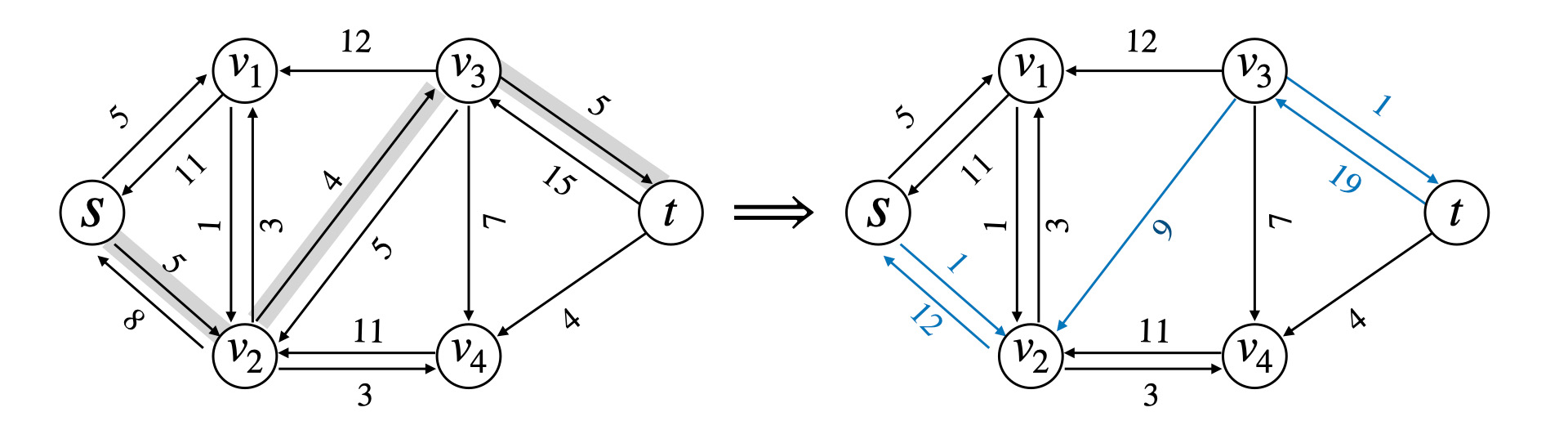
沿着增广路径走，注意 $G_f$ 中反向边流量增加
一条增广路径 $p$ 能够给 $G$ 每条边增加的流量最大值为路径 $p$ 的残存容量
$$ c_f(p) = \min \{c_f(u, v) : (u, v)\ \text{属于路径} \ p \} $$

引理
$G=(V, E)$ 为一个流网络，设 $f$ 为 $G$ 中的一个流，设 $p$ 为残量网络 $G_f$ 中的一条增广路径
$$ f_p(u, v) = \begin{cases} c_f(p) && \text{若} \ (u, v) \ \text{在} \ p \text{上} \\\ 0 && \text{其他} \end{cases} $$
$f_p$ 是残量网络 $G_f$ 中的一个流，$|f_p| = c_f(p) > 0$

流网络的切割

一个流是最大流当且仅当残量网络中不包括任何增广路径
为了证明这个算法的正确性，先引入流网络切割的概念

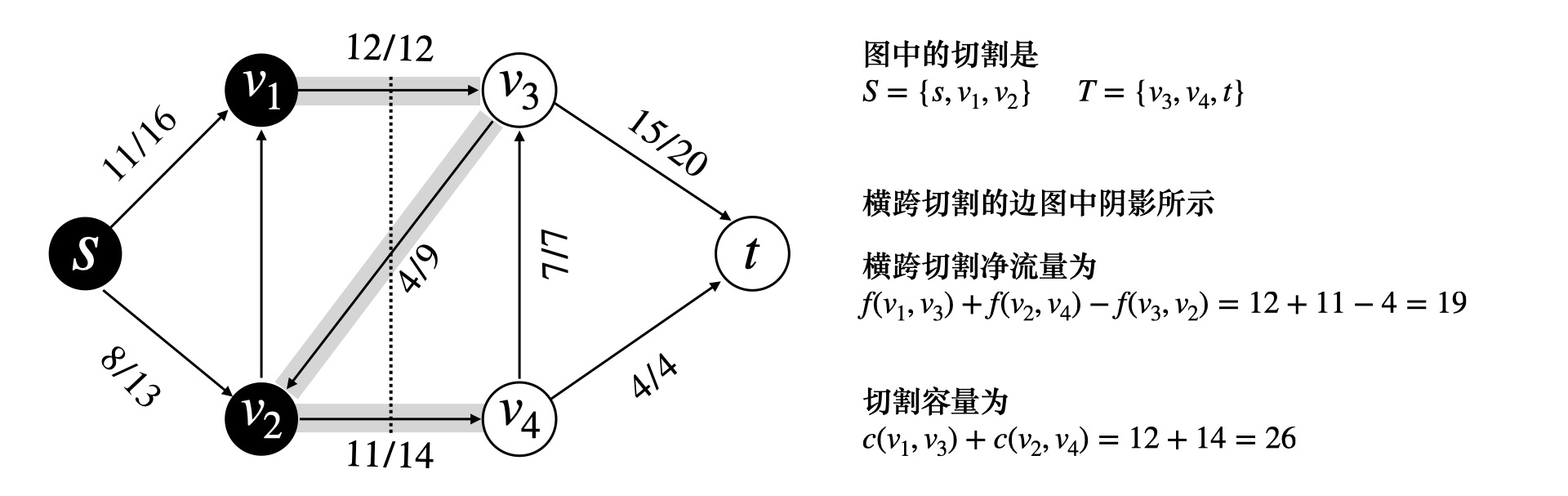
切割 $(S, T)$ 将流网络划分成了 $S$ 和 $T = V-S$ 两个集合
其中满足 $s \in S$, $t \in T$
净流量
$$ f(S, T) = \sum_{u \in S} \sum_{v \in T} f(u, v) - \sum_{u \in S} \sum_{v \in T}f(v, u) $$
割的容量
$$ c(S, T) = \sum_{u \in S} \sum_{v \in T} c(u, v) $$
引理
设 $f$ 为流网络 $G$ 的一个流，$(S, T)$ 为流网络的任意切割，则横跨任意切割$\forall \ (S, T)$ 的净流量总相同
$f(S, T) = |f|$

根据流量守恒
$\forall \ u \in V- \{s, t\}$
$$ \sum_{v \in V} f(u, v) - \sum_{v \in V} f(v, u) = 0 $$
对 $u \in S - \{s\}$ 进行求和
$$ \sum_{u \in S - \{s\}}\left( \sum_{v \in V}f(u, v) - \sum_{v \in V}f(v, u) \right) = 0 $$
由 $|f|$ 的定义
$$ |f| = \sum_{v \in V} f(s, v) - \sum_{v \in V} f(v, s) + \sum_{u \in S - \{s\}}\left( \sum_{v \in V}f(u, v) - \sum_{v \in V}f(v, u) \right) $$
展开并且重新组合
$$ \begin{aligned} |f| &= \sum_{v \in V}f(s, v) - \sum_{v \in V}f(v, s) + \sum_{u \in S - \{s\}}\sum_{v \in V}f(u, v) - \sum_{u \in S - \{s\}} \sum_{v \in V} f(v, u) \\\ &= \sum_{v \in V} \left(f(s, v) + \sum_{u \in S - \{s\}}f(u, v) \right) - \sum_{v \in V} \left( f(v, s) + \sum_{u \in S - \{s\}} f(v, u) \right) \\\ &= \sum_{v \in V}\sum_{u \in S} f(u, v) - \sum_{v \in V}\sum_{u \in S} f(v, u) \end{aligned} $$
将 $v \in V$ 拆点，拆成 $(v \in S) + (v \in T)$
$$ \begin{aligned} |f| &= \sum_{v \in S}\sum_{u \in S}f(u, v) + \sum_{v \in T} \sum_{u \in S}f(u, v) - \sum_{v \in S}\sum_{u \in S}f(v, u) - \sum_{v \in T} \sum_{u \in S}f(v, u) \\\ &= \sum_{v \in T} \sum_{u \in S}f(u, v) - \sum_{v \in T} \sum_{u \in S}f(v, u) \\\ &\quad + \left( \sum_{v \in S}\sum_{u \in S}f(u, v) - \sum_{v \in S}\sum_{u \in S}f(v, u) \right) \end{aligned} $$
括号中的求和项实际上是一样的，可以消去。由此
$$ |f| = \sum_{u \in S} \sum_{v \in T} f(u, v) - \sum_{u \in S} \sum_{v \in T}f(v, u) = f(S, T) $$

推论
流网络 $G$ 中任意流 $f$ 的值不能超过 $G$ 的任意切割的容量
$$ \begin{aligned} |f| &= f(S, T) = \sum_{u \in S} \sum_{v \in T}f(u, v) - \sum_{u \in S} \sum_{v \in T}f(v, u) \\\ &\leqslant \sum_{u\in S} \sum_{v \in T} f(u, v) \leqslant \sum_{u \in S}\sum_{v \in T}c(u, v) = c(S, T) \end{aligned} $$

流网络中最大流的值实际上等于一个最小切割的容量

最大流最小切割定理

设 $f$ 为流网络 $G=(V, E)$ 中的一个流，源点为 $s$，汇点为 $t$，以下条件等价
1. $f$ 是 $G$ 的一个最大流
2. 残量网络 $G_f$ 中不包括任何增广路径
3. $|f|=c(S, T)$，其中 $(S, T)$ 是流网络 $G$ 的某个切割

证明如下

$(1) \Rightarrow (2)$，这是显然的，因为如果有增广路径 $p$，那么可以让 $|f| \leftarrow |f| + |f_p|$
与 $|f|$ 是最大流矛盾
$(2) \Rightarrow (3)$，$G_f$ 中没有任何增广路径，也就是说，残量网络 $G_f$ 不存在任何 $s \to t$ 的路径
不妨令 $S = \{v \in V: \text{在} \ G_f \ \text{中存在一条从} \ s \ \text{到} \ v \ \text{的路径}\}, \quad T = V-S$
显然 $s \in S, \quad t \notin S$，因此划分 $(S, T)$ 作为流网络 $G$ 的一个切割
$u \in S, \quad t \in T$，也就是说 $(u, v) \in E$，必然有 $(u, v) \notin E_f$
也就是说 $c_f(u, v) = 0$
$$ c_f(u, v) = \begin{cases} c(u, v) - f(u, v) && \text{如果} \ (u, v) \in E \\\ f(v, u) && \text{如果} \ (v, u) \in E \\\ 0 && \text{其他} \end{cases} $$
也就是说，有 $f(u, v) = c(u, v)$，并且 $f(v, u) = 0$
因此
$$ f(S, T) = \sum_{u \in S}\sum_{v \in T}f(u, v) - \sum_{v \in T}\sum_{u \in S}f(v, u) = \sum_{u\in S} \sum_{v \in T}c(u, v) - \sum_{v \in T} \sum_{u \in S} 0 = c(S, T) $$
$(3) \Rightarrow (1)$
很显然 $|f| \leqslant c(S, T)$，$|f| = c(S, T)$ 取最大值

Ford-Fulkerson 算法

$\textbf{for} \ \forall \text{ edge}(u, v) \in G.E$
$\quad (u, v).f = 0$
$\textbf{while} \ \text{在残量网络} \ G_f \ \text{存在一条} \ s\to t \ \text{的增广路径} \ p$
$\quad c_f(p) = \min \{c_f(u, v) \quad (u, v) \in p\}$
$\quad \textbf{for} \ \forall \ \text{edge}(u, v) \in p$
$\quad \quad \textbf{if} \ (u, v) \in E: \quad (u, v).f = (u, v).f + c_f(p)$
$\quad \quad \textbf{else}: \quad (v, u).f = (v, u).f - c_f(p)$

算法分析

$\textbf{while}$ 循环中，使用 $\textbf{bfs}$ 找增广路，时间复杂度为 $O(V+E) = O(E)$
也就是说，每执行一次 $\textbf{while}$ 循环，所需要的时间复杂度为 $O(E)$
最坏情况每次 $c_f(p) = 1$，每次只增加 $1$，$\textbf{while}$ 循环最坏执行 $O(|f|)$ 次
时间复杂度为 $O(E |f|)$

Edmonds-Karp 算法

使用 $\textbf{bfs}$ 找增广路，选择 $s \to t$ 的最短路径作为增广路
其中每条边的权重为单位距离，$\delta_f(u, v)$ 表示残量网络 $G_f$ 中
$s \to t$ 的最短路径距离，其中每条边的权重为单位距离
时间复杂度 $O(VE^2)$

引理
$\text{Edmonds-Karp}$ 算法运行在流网络 $G=(V,E)$ 上，对于所有的节点 $v \in V - \{s, t\}$
残量网络 $G_f$ 的最短路径 $\delta_f(s, v)$ 随着流量的递增而单调增加

假设存在一个流量递增操作 $f \to f’$，对于 $G_f$ 中的边 $(u, v)$
$\delta_{f’} (s, u) \geqslant \delta_f (s, u)$，但
$\delta_{f’} (s, v) < \delta_f (s, v)$
另外根据 $\textbf{bfs}$ 过程，对于边 $E_{f’}(u, v)$ 我们有
$\delta_{f’}(s, v) = \delta_{f’}(s, u) + 1$

对于 $(u, v) \in E_{f’}$，那么一定有 $(u, v) \notin E_f$，否则的话
$$ \begin{aligned} \delta_{f}(s, v) &\leqslant \delta_{f}(s, u) + 1 \quad \text{因为} (u, v) \text{是可行势} \\\ &\leqslant \delta_{f’}(s, u) + 1 = \delta_{f’}(s, v) \end{aligned} $$
这与归纳假设矛盾
$(u, v) \in E_f, \quad (u, v)\notin E_{f’}$，意味着递增操作增加了 $v \to u$ 的流量，即检查了 $E_f(v, u)$
因为 $\text{Edmonds-Karp}$ 算法沿着最短路径增加流，所以 $G_f$ 中从 $s \to u$ 最短路径最后检查的边是 $(v, u)$
$$ \begin{aligned} \delta_{f}(s, v) &= \delta_{f}(s, u) - 1 \\\ &\leqslant \delta_{f’}(s, u) - 1 = \delta_{f’}(s, v)-2 \end{aligned} $$
这个与 $\delta_{f’}(s, v) < \delta_{f}(s, v)$ 矛盾

定理
$\text{Edmonds-Karp}$ 算法执行的流量递增操作总次数为 $O(VE)$
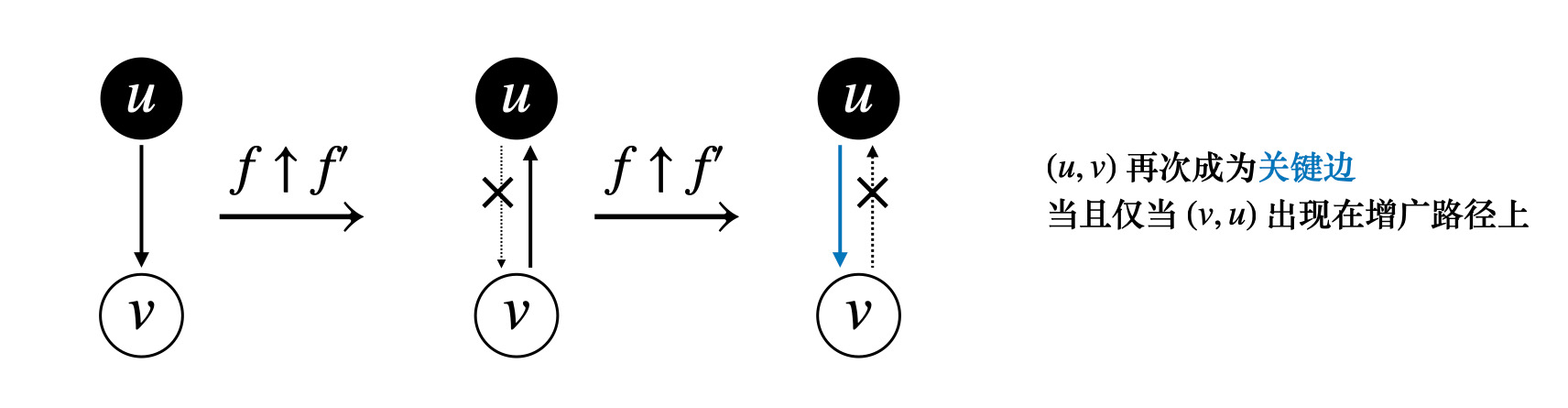
在残量网络 $G_f$ 中，对于增广路径 $p$，如果 $c_f(p) = c_f(u, v)$，$(u, v)$ 是增广路径的关键边
（在前面的图中，就是容量为 $4$ 的那条边）
对于 $|E|$ 中的每条边而言，其成为关键边的次数最多为 $|V|/2$ 次

沿着增广路径增加流，关键边从残量网络 $G_f$ 中消失，它再次成为关键边
只有当 $(u, v)$ 网络流量减小，也就是 $(v, u)$ 出现在增广路径上的时候，如下图
此时有
$\delta_{f}(s, v) = \delta_{f}(s, u) + 1$
$\delta_{f’}(s, u) = \delta_{f’}(s, v) + 1$
因为 $\delta_{f}(s, v) \leqslant \delta_{f’}(s, v)$，所以有
$\delta_{f’}(s, u) = \delta_{f’}(s, v) + 1 \geqslant \delta_{f}(s, v) + 1 = \delta_{f} (s, u) + 2$
从 $(u, v)$ 第一次成为关键边到下一次再成为关键边
$(s, u)$ 之间的距离至少增加了 $2$ 个单位，因为 $s \to u$ 最短路径不包括 $s, t$
所以二者之间的距离最多为 $|V|-2$
因此 $(u, v)$ 最多可以再成为关键边 $O(|V|/2)$ 次
关键边的总数为 $O(|E| \cdot |V|/2)$

算法实现

const int maxn = 1000 + 10, maxm = 20000 + 10;
const int inf = 0x3f3f3f3f;
int head[maxn], ver[maxm], edges[maxm], ne[maxm], tot = 1, n, m, S, T;
int d[maxn], pre[maxn], vis[maxn];

void add(int a, int b, int c) {
    ver[++tot] = b; edges[tot] = c; ne[tot] = head[a]; head[a] = tot;
}

bool bfs() {
    memset(vis, 0, sizeof vis);
    memset(d, 0, sizeof d);
    memset(pre, 0, sizeof pre);
    queue<int> q;

    vis[S] = 1, d[S] = inf, q.push(S);
    while (q.size()) {
        int x = q.front(); q.pop();
        for (int i = head[x]; i; i = ne[i]) {
            int y = ver[i];
            if (!vis[y] && edges[i] > 0) {
                vis[y] = true;
                d[y] = min(d[x], edges[i]);
                pre[y] = i;
                if (y == T) return true;
                q.push(y);
            }
        }
    }
    return false;
}

void EK() {
    int res = 0;
    while (bfs()) {
        res += d[T];
        for (int i = T; i != S; i = ver[pre[i] ^ 1]) {
            int id = pre[i];
            edges[id] -= d[T], edges[id ^ 1] += d[T];
        }
    }
    printf("%d\n", res);
}

int main() {
    //freopen("input.txt", "r", stdin);
    scanf("%d%d%d%d", &n, &m, &S, &T);
    for (int i = 0; i < m; i++) {
        int a, b, c;
        scanf("%d%d%d", &a, &b, &c);
        add(a, b, c);
        add(b, a, 0);
    }

    // Edmonds karp
    EK();
}