题目描述

给定 N 个加号、M 个减号以及 N+M+1 个整数 A1,A2,⋅⋅⋅,AN+M+1，小明想知道在所有由这 N 个加号、M 个减号以及 N+M+1个整数凑出的合法的后缀表达式中，结果最大的是哪一个？
请你输出这个最大的结果。
例如使用 123+−，则 “23+1−” 这个后缀表达式结果是 4，是最大的。

输入格式
第一行包含两个整数 N和 M。
第二行包含 N+M+1
个整数 A1,A2,⋅⋅⋅,AN+M+1。

输出格式
输出一个整数，代表答案。

数据范围
0≤N,M≤105,
−109≤Ai≤109

样例

输入样例：

1 1
1 2 3

输出样例：

4

拓展：后缀表达式 后缀表达式
二叉树的前序，中序，后序，就分别代表前缀表达式，中缀表达式，后缀表达式
逆波兰表达式：
内部结点：运算符。
叶子结点：操作数。

普遍的都是 知道了中序和后序，或者知道了中序和前序才能推出一棵二叉树，但是这知道叶子结点都是操作数，内部结点是操作数，仅仅知道后序就可以推出来一颗二叉树了。
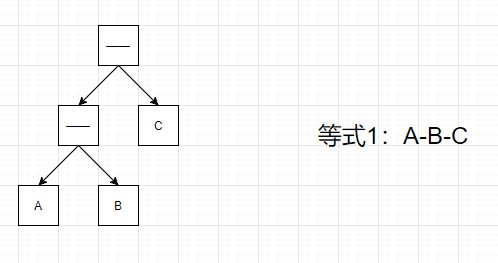
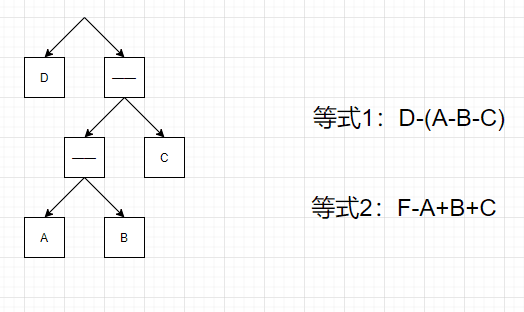
不是说m个负号，就要减去m个数，我们可以调整运算的顺序，等价于中缀表达式加括号(),
后缀表达式里不能加括号，只能调整运算顺序。给出了可以通过调整后缀表达式的顺序，起到在对应的中缀表达式中的任意位置加括号的效果。

#include <iostream>
#include <cstring>
#include <cstdio>
#include <algorithm>
#include <cmath>
#define LL long long 
using namespace std;
int n,m;
int a[200010];//注意数据范围,n,m的范围是[10000],题上存的数的个数是n+m+1，所以应该是2倍的100000+1范围 
int main(){
scanf("%d%d",&n,&m);
long long k=n+m+1;
for(int i=0;i<k;i++){
    scanf("%d",&a[i]);
}
sort(a,a+k);
long long res=0;
if(!m){//如果没有负号，那么就全部都是正的，直接从头加到尾即可 
    for(int i=0;i<k;i++){
        res+=a[i];
    }
}else{
    res=a[k-1]-a[0];
    for(int i=1;i<k-1;i++){
    res+=abs(a[i]);
}   
}
printf("%lld\n",res);
    return 0; 
}