思路:我们令s[i]来表示前i个数的和，那么L~R的和就是s[R]-s[L],如果L~R的和是偶数，说明s[R]和s[L]的值应该都是奇数或者都是偶数，只要我们推出前面确定的奇偶性与当前给的奇偶性不同，则产生矛盾

解法一:带边权并查集

我们用d[i]来表示当前节点与父亲节点的关系，0表示奇偶性相同，1表示奇偶性不相同
那么再进行路径压缩时候，我们怎么将当前节点i直接与根节点root产生关联呢
当父亲节点已经连接根结点时候，那么d[i]与根节点关系不就变成了d[i]=d[i]+d[fa[i]]了吗，我们通过层层递归，先将父亲节点连向根节点，再更改当前节点的d[i]值就好了

如果给出a b 那么我们怎么找到a和b的关系 假设a和b 的父亲节点为pa pb
1.pa==pb 我们通过向量的方式理解

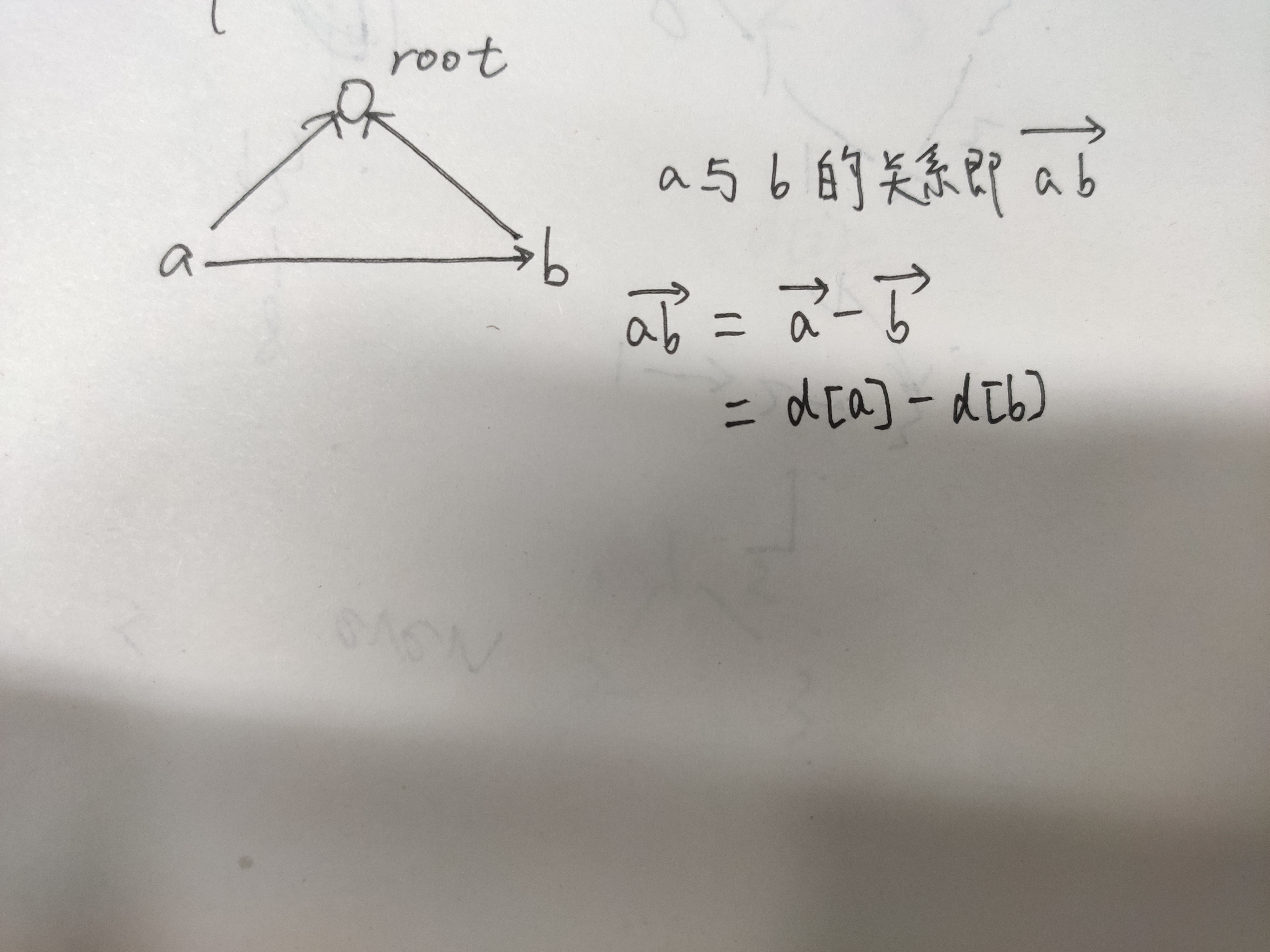
我们通过算出((d[a]-d[b])%2+2)%2，与题目给出条件看是否矛盾

2.pa!=pb，此时说明两者还没产生关联，我们需要将fa[pa]=pb,那么pa和pb的关系又是什么呢
同样也通过向量来理解

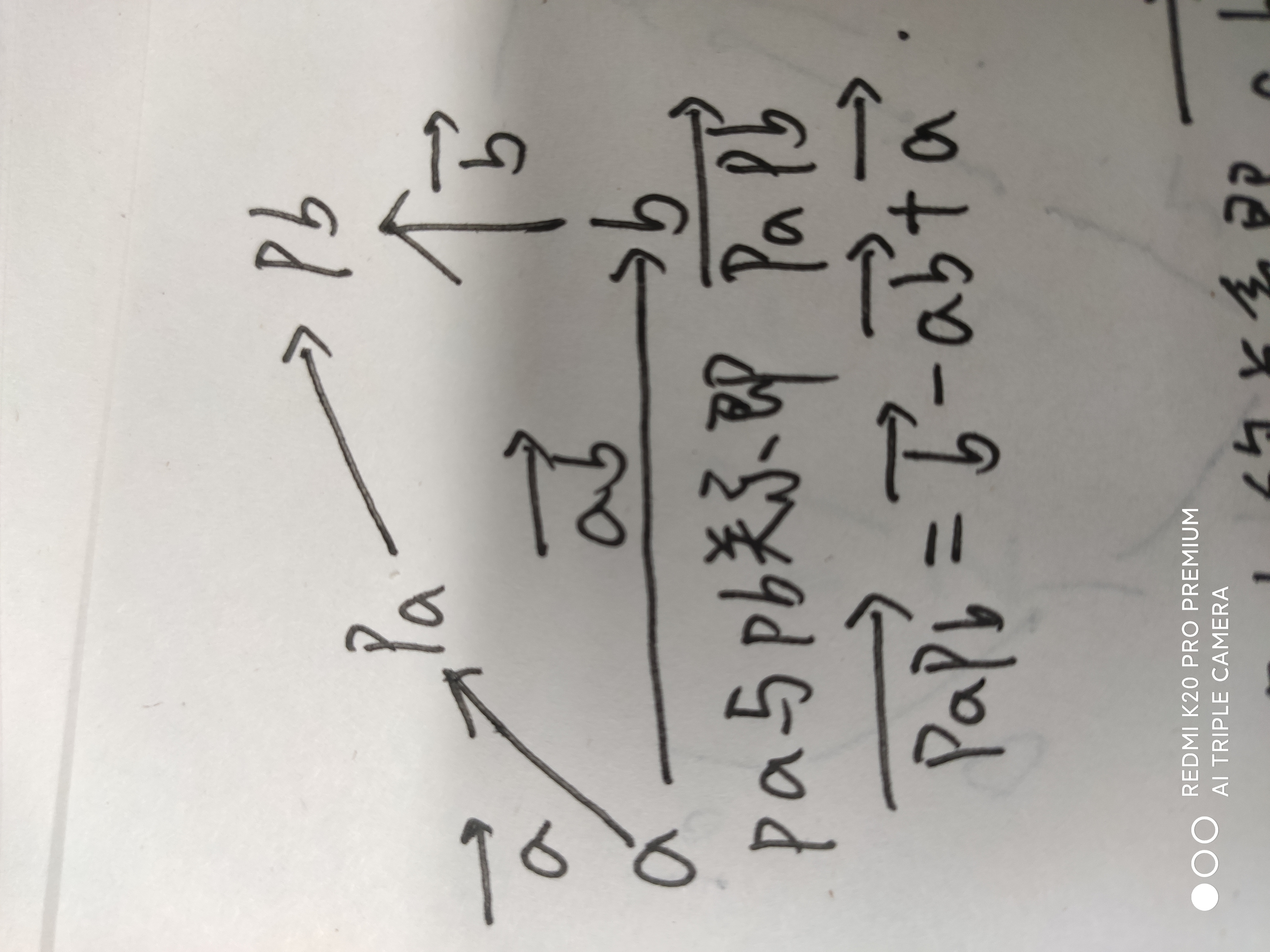
这样我们就完成了，具体代码

#include<bits/stdc++.h>
using namespace std;

const int N=10000+5;

unordered_map<int,int>mp;

int fa[N*2],d[N*2];
int k;

int get(int x)
{
    if(!mp.count(x)) mp[x]=++k;
    return mp[x];
}

int find(int x)
{
    int r=x;
    while(r!=fa[r])
      {
        int root=find(fa[r]);
        d[x]^=d[fa[x]];
        fa[x]=root;
      }
    return r;
}

void merge(int a,int b,int c)
{
    int pa=find(a);
    d[pa]=d[a]^c;
    fa[pa]=b;
}

int main()
{
    int n,m;
    cin>>n>>m;
    int res=m;

    for(int i=1;i<=N*2;i++) fa[i]=i;
    for(int i=1;i<=m;i++)
      {
        int l,r;
        string s;
        cin>>l>>r>>s;
        l=get(l-1),r=get(r);

        int pl=find(l),pr=find(r);
        if(pl==pr)
          {
            if(s=="even"&&d[pl]^d[pr]==1) break;
            if(s=="odd"&&d[pl]^d[pr]==0) break;
          }
        int t=0;
        if(s=="odd") t=1;
        merge(l,r,t);
        res=i; 
      }
    cout<<res<<endl;
    return 0;
}

解法二：扩展域并查集
我们用a,a+n来表示a是奇数和偶数两种状态
如果a和b奇偶性相同 则a可能是奇数，也可能数偶数，需要合并 a和b 以及 a+n和b+n;
如果奇偶性不相同，当a是奇数是，b为偶数，此时需要合并a 和 b+n
当a是偶数时，b时奇数，合并a+n 和 b

#include<bits/stdc++.h>
using namespace std;

const int N=2e4+10,base=N/2;
typedef long long ll;
int fa[N];
unordered_map<ll,ll>mp;
int k;

int get(int x)
{
    if(mp.count(x)==0) mp[x]=++k;
    return mp[x];
}

int find(int x)
{
    if(x!=fa[x]) fa[x]=find(fa[x]);
    return fa[x];
}

void merge(int a,int b)
{
    fa[find(a)]=find(b);
}

int main()
{
    int n,m;
    cin>>n>>m;

    n=base;
    for(int i=0;i<N;i++) fa[i]=i;
    int res;
    for(int i=1;i<=m;i++)
      {
        int a,b;
        string type;
        cin>>a>>b>>type;
        a=get(a-1),b=get(b);

        if(type=="even")
          {
            if(find(a)==find(b+n)) break;
            merge(a,b);
            merge(a+n,b+n);
          }
        else
          {
            if(find(a)==find(b)) break;
            merge(a+n,b);
            merge(a,b+n);
          }
        res=i;
      }
    cout<<res<<endl;
    return 0;
}