算法思路

prim算法的思路其实非常简单，我们一起来模拟一下你就懂了，我们先跟着样例画一个图

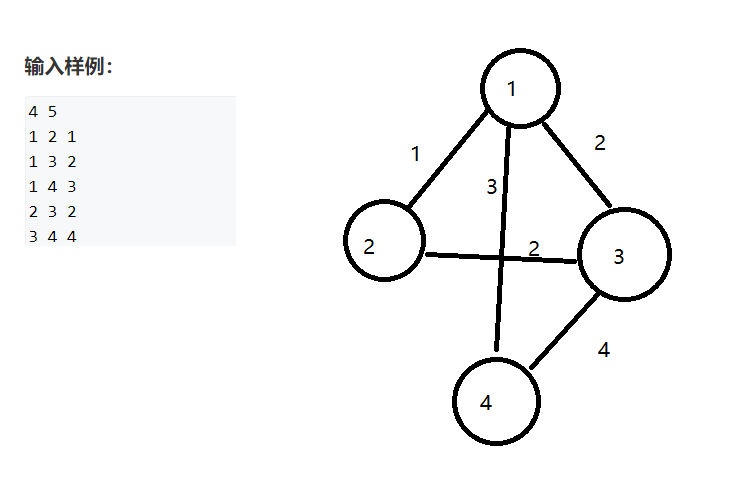
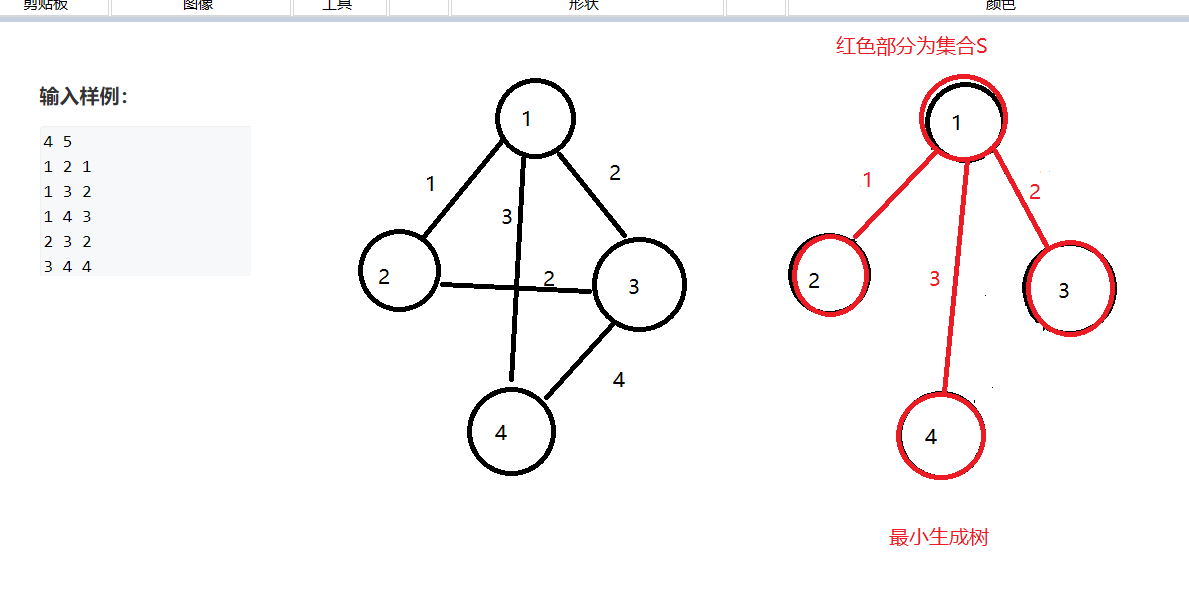
好，现在开始，假设我们有个集合S，Prim的思路就是依次把图中距离集合最小的点加入到集合中，直到图中所有点都加到集合中，最小生成树就出来了。
第一步，我们的集合S现在是空的,先随意选个点加入集合中,既然是随意，那就决定是你了，1号点

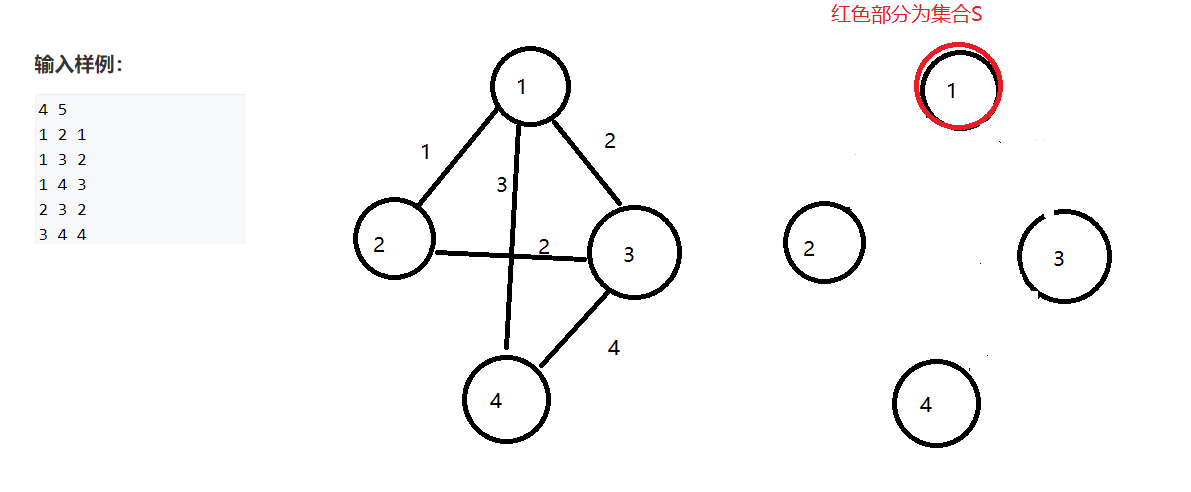
然后依次把距离集合S最近的点加入到S中去，现在距离S最近的是2号点距离是1，我们把2号点连着这个边并入集合S中去

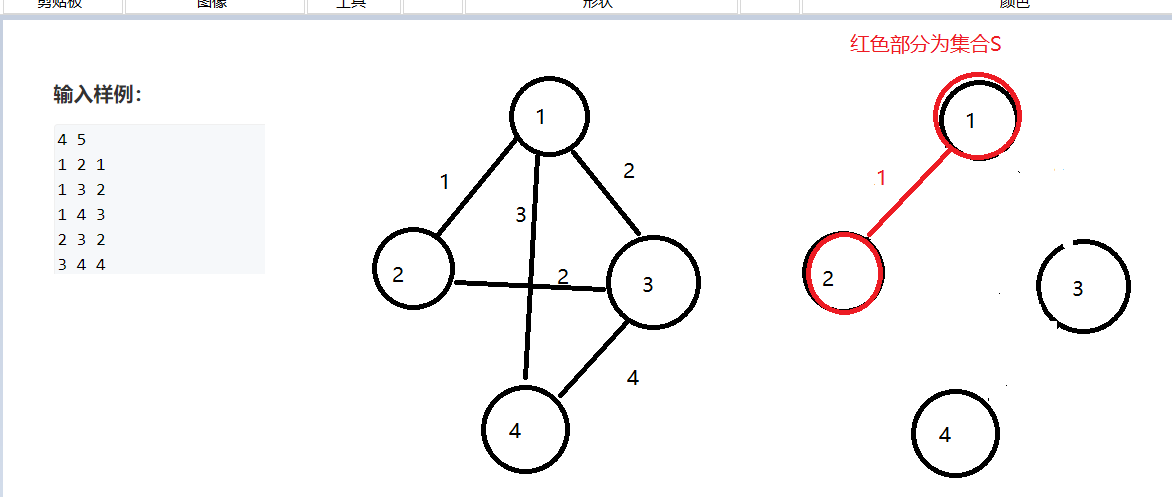
现在距离集合S最近的是3号点，但是有两条边都满足条件，那这个时候我们选择哪一条边都是可以的，也能得出最小生成树不是唯一的，我们把3号点和其中一条边并入集合中去

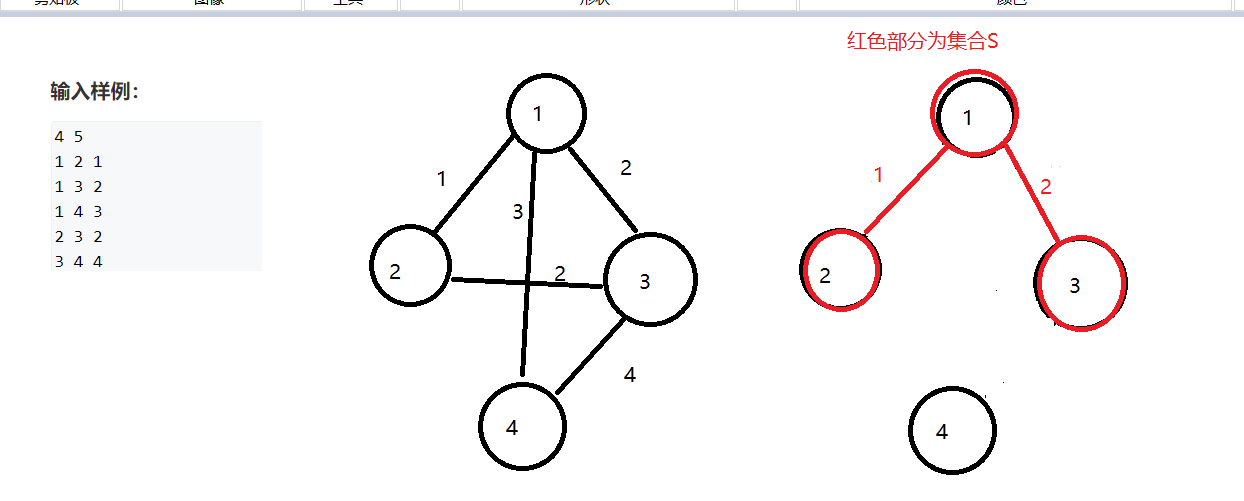
还剩下最后的4号点，它距离集合S最近的距离是3我们把4号点连同这条边并入集合S中去之后就得到最小生成树了

代码怎么写

算法思路不难，那么代码应该怎么写呢，首先是图的存储，我们选用邻接矩阵来存储。

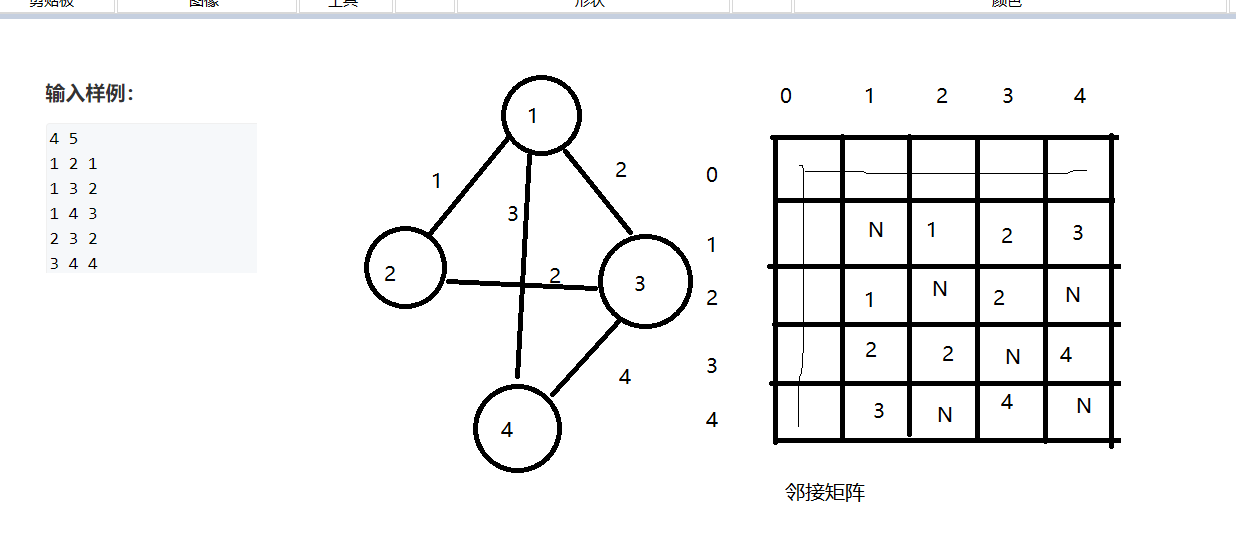
开一个二维数组g即可存储这个邻接矩阵了,注意下标都是从1开始的。其中g[i][j]表示结点i到结点j的边的长度，若是长度为N（无穷大）就代表两点之间不存在边。
state[i] 存储结点i是否在集合S内
distance[i] 存储结点i到集合S的距离，但是注意这个距离是动态的，当一个结点加入到S中去的时候，会引起别的distance变化，比如下面这种

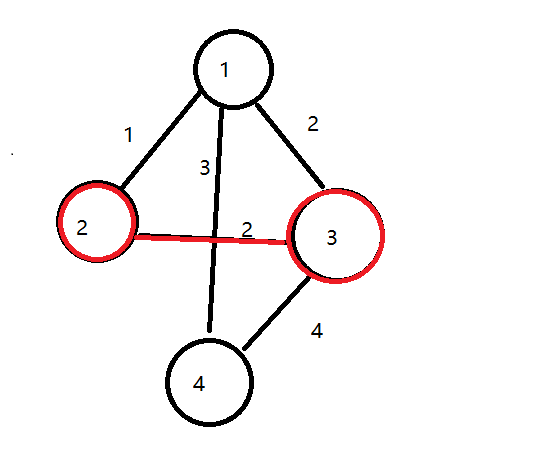
此时distace[4]=4,但是当结点1加入集合后distacne[4]就应该变成3,由此也可以推出distacne的更新公式，当有结点t加入集合中时，应该更新distance[i] = Math.min(distance[i],g[t][i])。

完整java代码

import java.util.Arrays;
import java.util.Scanner;

public class Main {

    static int INF = 0x3f3f3f3f;

    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        int n = scanner.nextInt(), m = scanner.nextInt();
        int[][] g = new int[n + 1][n + 1]; // 邻接矩阵
        int[] distance = new int[n + 1]; // 记录结点i距离集合的距离
        boolean[] state = new boolean[n + 1]; // 标注结点i（下标从1开始）是否在当前选中的集合中

        //邻接矩阵和距离数组的初始值都应是正无穷
        Arrays.fill(distance, INF);
        for (int i = 0; i <= n; i++) {
            Arrays.fill(g[i], INF);
        }
        // 构造邻接矩阵
        for (int i = 0; i < m; i++) {
            int a = scanner.nextInt(), b = scanner.nextInt(), w = scanner.nextInt();
            g[a][b] = Math.min(g[a][b], w);
            g[b][a] = g[a][b];
        }

        int res = prim(n, m, g, distance, state);

        if (res == INF)
            System.out.println("impossible");
        else
            System.out.println(res);
        scanner.close();
    }

    private static int prim(int n, int m, int[][] g, int[] distance, boolean[] state) {
        int res = 0;
        for (int i = 0; i < n; i++) {
            // 找到选中集合外距离集合最小的点
            int indexOfMin = -1;
            for (int j = 1; j <= n; j++) {
                if (!state[j] && (indexOfMin == -1 || distance[j] < distance[indexOfMin]))
                    indexOfMin = j;
            }
            // 将距离集合最小的点加入到集合中
            state[indexOfMin] = true;
            // 将选中边加到结果中，除了第一条
            if (i != 0)
                res += distance[indexOfMin];
            if (i != 0 && distance[indexOfMin] == INF)
                return INF;
            // 将距离集合最小的点加入到集合中后可能会引起别的距离变化
            for (int j = 1; j <= n; j++) {
                if (!state[j]) {
                    distance[j] = Math.min(distance[j], g[indexOfMin][j]);
                }
            }
        }
        return res;
    }

}