题目描述

给定一个n个点m条边的有向图，点的编号是1到n，图中可能存在重边和自环。

请输出任意一个该有向图的拓扑序列，如果拓扑序列不存在，则输出-1。

若一个由图中所有点构成的序列A满足：对于图中的每条边(x, y)，x在A中都出现在y之前，则称A是该图的一个拓扑序列。

输入格式
第一行包含两个整数n和m

接下来m行，每行包含两个整数x和y，表示存在一条从点x到点y的有向边(x, y)。

输出格式
共一行，如果存在拓扑序列，则输出任意一个合法的拓扑序列即可。

否则输出-1。

数据范围
1≤n,m≤10^5

样例

输入样例：
3 3
1 2
2 3
1 3
输出样例：
1 2 3

算法1

(暴力枚举) $O(n^2)$

有向图才有拓扑序列
有向无环图一定存在拓扑序列
入度，出度
如何求拓扑序列(所有边都是从前指向后)
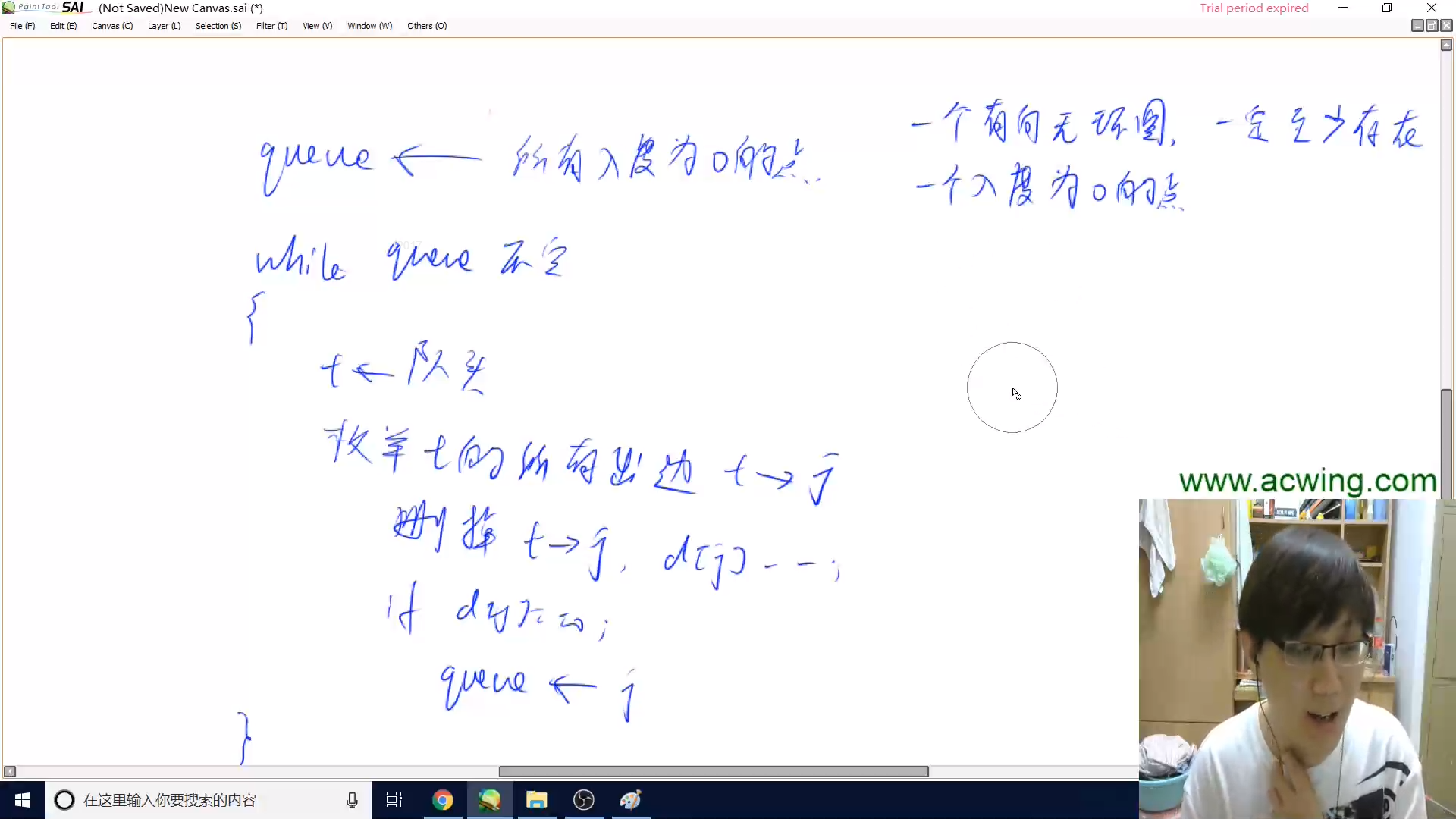
入度为0，没有任何一条边指向该点。所有入度为0的点都可以排在最前面。
所有入度为0的点都要入队
取出队头t，枚举t的所有出边t->j
删掉t->j,j的入度减1
一个有向无环图，一定存在一个入度为0的点

python 代码

import collections

N = 100010
e = [0] * N         #下标为边，值为边指向的点
ne = [0] * N        #下标为边，值为邻接表对应的下一条边
h = [-1] * N        #下标为点，值为该点邻接表的第一条边。-1表示边不存在
d = [0] * N         #下标为点，值为改点的入度
idx = 0
ans = []

def add(a,b):
    global idx
    e[idx] = b          #编号为idx的边指向b
    ne[idx] = h[a]      #idx的下一条边指向a点的原来邻接表的第一条边
    h[a] = idx          #a点邻接表的第一条边更新为idx
    idx += 1            #边的编号+1

def topsort():
    k = 0
    q = collections.deque()
    for i in range(1,n+1):
        if not d[i]:
            q.append(i)     #遍历初始化之后的d[],入度为0的进队。

    while q:
        t = q.popleft()     #取出队头
        k+=1                #记录有多少点进队(出队)
        ans.append(t)       #记录答案，按出队顺序 就是拓扑序列
        i = h[t]
        while i != -1:      #遍历t的所有出边
            j = e[i]        #j为i边指向的点
            d[j] -= 1       #删除t的一条出边（该边指向j，所以也是j的入边）
            if d[j] == 0:   #如果删除j的入边后j的入度为0，则j入队
                q.append(j)
            i = ne[i]
    return k == n


if __name__ == "__main__":
    n,m = map(int,input().split())

    for i in range(m):
        a,b = map(int,input().split())
        add(a,b)
        d[b] += 1       #a指向b的一条边，b的入度+1
    if topsort():
        print(" ".join(str(i) for i in ans))
    else:
        print(-1)