题目描述

原题

输入一个长度为n的整数数列，从小到大输出前m小的数。

输入格式
第一行包含整数n和m。

第二行包含n个整数，表示整数数列。

输出格式
共一行，包含m个整数，表示整数数列中前m小的数。

数据范围
1≤m≤n≤105，
1≤数列中元素≤109
输入样例：
5 3
4 5 1 3 2
输出样例：
1 2 3

算法 堆

1. 堆:
   是一个完全二叉树:除最后一层,上面的结点都是2个,最后一层从左到右排列.

2. 堆基本的操作：

   1. 插入一个数：heap[++size] = x ; up(size);
   2. 求集合中的最小值:heap[1]
   3. 删除最小值:heap[1] = heap[size] ; size– ; down( 1 );
      (后面两个操作STL容器里面的堆无法直接实现)
   4. 删除任意一个元素: heap[k]=heap[size]; size–;down(k);up(k);(down,up只会有运行一个，因为k这个点要么大于往下走，要么小于往上走)
   5. 修改任意一个元素heap[k] = x ; down(k); up(k);

3. 小根堆性质:
   每一个结点都是小于等于左右孩子结点.

4. 堆的存储方式:
   一维数组，1是根结点，x的左儿子为2x, 右儿子为2x+1.
   （如果下标从0开始。就会发现2x即左儿子还是0，冲突）

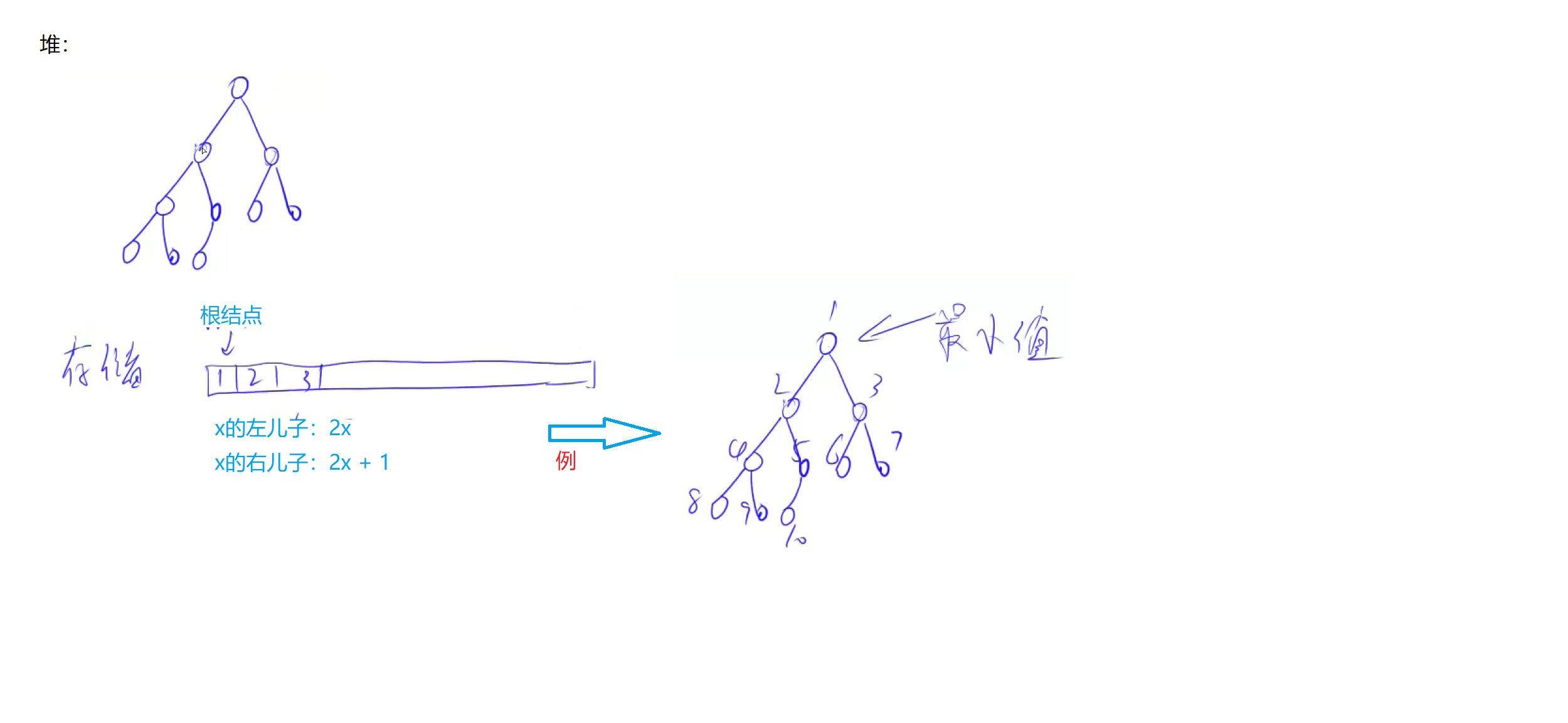
本题只用到了第三个，删除最小值，所以只要实现down操作。

2022-4-4：更新down操作从n/2处开始的证明。

时间复杂度

down操作、插入删除和树的高度有关，所以是O(logn）；求最小值O(1)。

参考文献

y总讲解视频

C++ 代码

#include <iostream>
#include <algorithm>
#include <cstring>

using namespace std;

const int N = 100010;
//h就是heap，堆数组  length堆里面有多少个元素
int h[N] , length;
//n有多少个数  m输出前面m个数
int n , m;

//down操作：把一个元素往下移
void down(int u){
    //用t来表示三个结点之间的最小值：即当前结点和它的左右孩子结点
    int t = u;
    //先看一下左孩子是否在堆中 ， 并进行判断是不是比此时的t小，是就更新t
    if(u * 2 <= length && h[u * 2] < h[t]) t = u * 2;
    //下面的右孩子结点同理
    if(u * 2 + 1 <= length && h[u * 2 + 1] < h[t]) t = u * 2 + 1;
    //最后t存储的就是三个结点之间的最小值
    //如果u！=t ， 说明u就不是最小值
    if(u != t){
        //交换
        swap(h[u] , h[t]);
        //递归处理
        down(t);
    }
}

int main(){
    // 输入h数组
    scanf("%d %d" , &n , &m);
    for(int i = 1; i <= n ;i++) scanf("%d" , &h[i]);
    //初始化长度
    length = n;

    //从n/2开始down，也就是从非叶结点开始进行元素下移的操作,建堆
    for(int i = n / 2 ; i  ;i--)down(i);


    while(m--){
        //输出当前的堆顶元素
        printf("%d " , h[1]);
        //输出后，要删除堆顶元素.把最后元素赋给堆顶元素
        h[1] = h[length];
        //堆的长度对应相减
        length--;
        //把堆顶元素往下移，重新进行排序
        down(1);
    }
    return 0;
}