算法分析

假设波动序列第一个值为$x$，记每次操作$d_i\in \lbrace+a,-b\rbrace $。
根据波动序列的性质，每一项比前一项增加a或者减少b，

构成波动序列: $x， x + d_{n - 1}， x + d_{n - 1} + d_{n - 2}， x + d_{n - 1} + d_{n - 2} + d_{n - 3}， …， x + d_{n - 1} + d_{n - 2} + d_{n - 3} + … + d_1$

将等式变形并使用n，s，$d_i$将x表示出来：
$x = \cfrac{s - (n - 1)d_{n - 1} - (n - 2)d_{n - 2} - …-d_1}{n} $

波动序列：对于序列{$d_1, d_2, …, d_{n - 1}$} 中每一项选择是{+a, -b}。n - 1次选择构成的选择序列对应一个不同的波动序列，每个选择序列都是由n - 1次操作组合而来，所以是一个组合问题。

01背包问题：每件物品都有选或不选的两种策略，n件物品选or不选构成一个长度为n的决策序列，一个长度为n的决策序列对应一种选择方案，每种方案都是由选或不选组合而来，所以是一个组合问题。

闫式dp分析

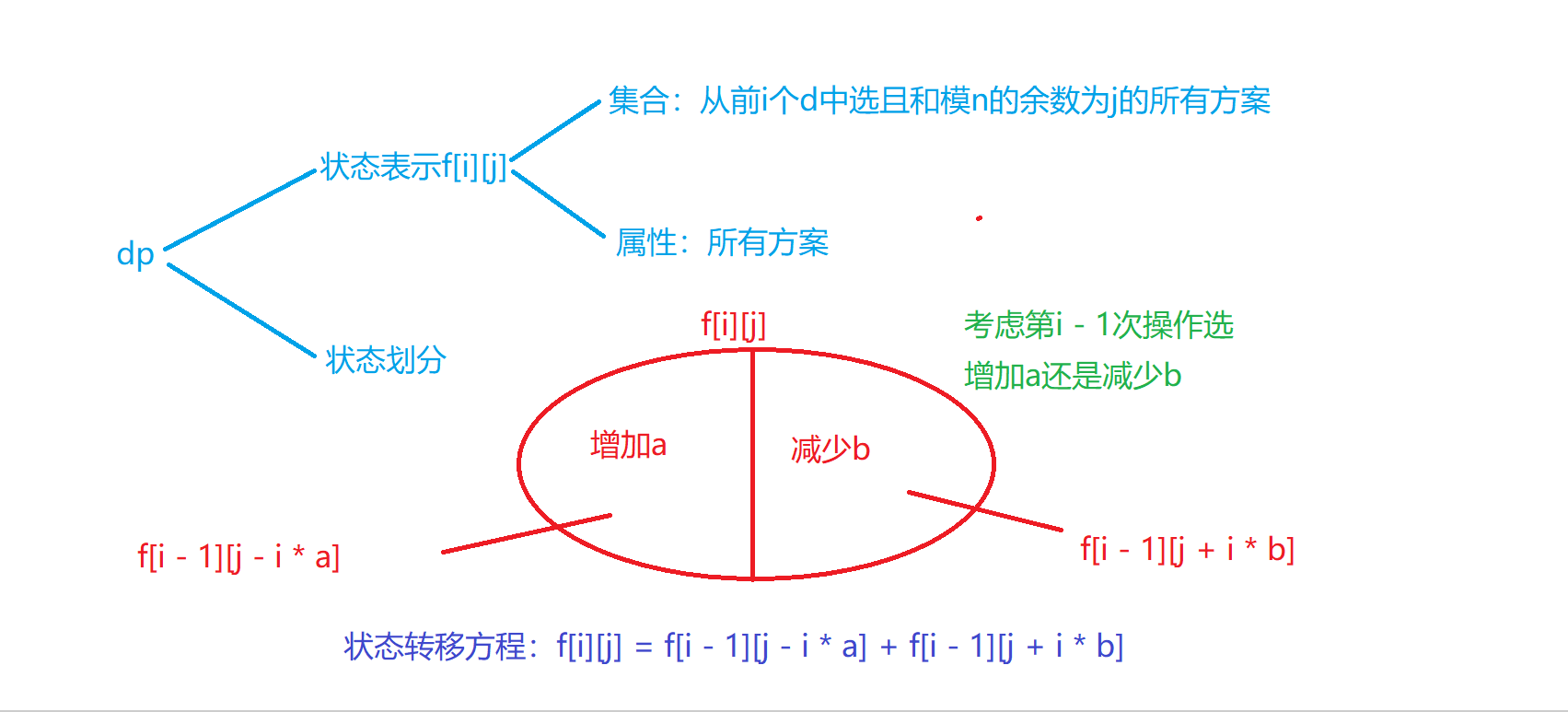
细节

• 组合问题

假设波动序列只有三个数，初始值为x，每次操作在{+a, -b}中选择，那么可以操作的序列有四种情况{+a, +a}, {+a, -b}, {-b, +a}, {-b, -b}，每一种操作的情况对应一个不同的波动序列，每一种情况都是通过组合+a 或 -b两种操作组合而来，所以波动数列的本质就是组合问题。

• $(n - 1)d_{n - 1} + (n - 2)d_{n - 2} + … + d_{1}$

对于每个$d_i$都是两种操作{+a, -b}之一，对于第一次是$d_1$还是$d_{n - 1}$都是无所谓的。如果按照$d_1$，$d_2$, …,这样的顺序操作最终的到的结果是$(n - 1)d_1 + (n - 2)d_2 + (n - 3)d_3 + … + d_{n - 1}$。

结果与初始化

• 最终结果

首先令 sum = $(n - 1)d_{n - 1} + (n - 2)d_{n - 2} + … + d_{1}$

s 与 sum 同余的所有方案:f[n - 1][s % n]
为什么是n - 1，而不是n? 因为是从序列的第二项开始操作，一直到序列的第n项，总共操作n - 1次，所以是n - 1

• 初始化

f[0][0] = 1，从0次操作中选， sum模n的结果为0，只有一种方案，所以初始化为1，其他情况为非法方案，初始化为0

代码

#include<iostream>
using namespace std;
const int N = 1010, mod = 100000007;
int f[N][N];
int get_mod(int a, int b){//求a对b进行取模，无论a是正数还是负数
    return (a % b + b ) % b;
}
int main(){
    int n, s, a, b;
    scanf("%d %d %d %d", &n, &s, &a, &b);

    f[0][0] = 1;

    for(int i = 1; i < n; i ++){
        for(int j = 0; j < n; j ++)//对n取模只有0~n-1
        f[i][j] = (f[i - 1][get_mod(j -i * a, n)] + f[i - 1][get_mod(j + i * b , n)])%mod;
    }
    printf("%d\n", f[n - 1][get_mod(s, n)]);//只进行n - 1次操作
    return 0;
}