算法1 贪心

1. 先考虑最远到哪个鱼塘，把路上的时间预先减掉，剩下的就是完全用于钓鱼的时间
   • 注意这里不用考虑折返的情况，因为如果折返前一个池塘钓鱼可以得到更优解，那么完全可以在之前就接着钓
2. 因为一分钟计算一次鱼的数量，而每个鱼塘在第几分钟能钓到的鱼数量是可以确定的，且时间越靠前的数量越多，按样例打个表格
   
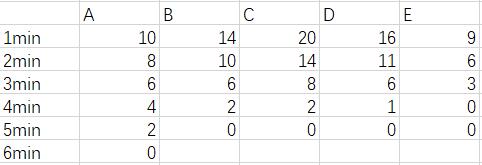
3. 记完全用于钓鱼的时间为$t$，因为所用到的鱼塘的路程耗费时间已经是减过的，而一分钟钓一次鱼，所以只需在用到的池塘选择不多于$t$个的前几个数，它们的总和就是最终能钓到的鱼总数
   • 注意是每个池塘的前几个数，而且连续，因为有时间关系
   • 实际上，计算的是总和，所选的数应尽可能大，而越靠前的数值越大，最优解也不会存在不连续的情况
4. 无关顺序，取最大的前几个，因此考虑使用优先队列，或者放进ArrayList再进行排序
5. 虽然用的是优先队列，但是时间复杂度并没有什么优化，还不如ArrayList+排序，有优化的优先队列需要存当前数值和衰减速度

代码

import java.util.*;
import java.lang.*;

public class Main {
    static Scanner scanner = new Scanner(System.in);

    static int n, T, N = 110;  // 鱼塘个数 截止时间
    static int[] a = new int[N], da = new int[N], ta = new int[N];  // 初始个数 衰减速度 移动时间

    public static void main(String[] args) {
        PriorityQueue<Integer> pq = new PriorityQueue<>((o1, o2) -> o2 - o1);  // 大根堆
        n = scanner.nextInt();
        for (int i = 1; i <= n; i++) a[i] = scanner.nextInt();
        for (int i = 1; i <= n; i++) da[i] = scanner.nextInt();
        for (int i = 1; i < n; i++) ta[i] = scanner.nextInt();
        T = scanner.nextInt();

        int res = 0;
        for (int k = 1; k <= n; k++) {  // 枚举最远到达的鱼塘
            int t = T, total = 0;
            for (int i = 1; i < k; i++) t -= ta[i];  // 计算余下时间 这里可以用前缀和优化
            for (int i = 1; i <= k; i++)
                for (int j = a[i]; j > 0; j -= da[i]) pq.add(j);  // 加入优先队列
            while (t-- > 0 && !pq.isEmpty()) total += pq.poll();  // 获取不超过t个的前几个数
            pq.clear();  // 一轮枚举 清空队列
            res = Math.max(res, total);  // 多种方案取最大值
        }

        System.out.println(res);
    }
}

算法2 优先队列

1. 思路同上，发挥优先队列的优势，在添加鱼塘可获得的鱼总数时，只放入所有能到达的鱼塘当前分别可获得的鱼条数
2. 每次同样取最大的一个数，但现在省略了枚举，且队列的元素个数较少，访问速度快

代码

import java.util.*;
import java.lang.*;

public class Main {
    static Scanner scanner = new Scanner(System.in);

    static class Pair {
        public int l, r;

        public Pair(int l, int r) {
            this.l = l;
            this.r = r;
        }
    }

    static int n, T, N = 110;  // 鱼塘个数 截止时间
    static int[] a = new int[N], da = new int[N], ta = new int[N];  // 初始个数 衰减速度 移动时间

    public static void main(String[] args) {
        PriorityQueue<Pair> pq = new PriorityQueue<>((o1, o2) -> o2.l - o1.l);  // 大根堆
        n = scanner.nextInt();
        for (int i = 1; i <= n; i++) a[i] = scanner.nextInt();
        for (int i = 1; i <= n; i++) da[i] = scanner.nextInt();
        for (int i = 2; i <= n; i++) ta[i] = ta[i - 1] + scanner.nextInt();  // 优化为前缀和
        T = scanner.nextInt();

        int res = 0;
        for (int k = 1; k <= n; k++) {  // 枚举最远到达的鱼塘
            int t = T - ta[k], total = 0;
            for (int i = 1; i <= k; i++) pq.add(new Pair(a[i], da[i]));  // 添加鱼塘初始值
            while (t > 0) {
                Pair temp = pq.poll();
                total += temp.l;  // 取最大的一个数 加到总和 并更新当前获得值 添加回队列
                pq.add(new Pair(Math.max(0, temp.l - temp.r), temp.r));
                t--;  // 每钓上一次鱼 时间-1
            }
            pq.clear(); // 枚举完一轮 清空队列
            res = Math.max(res, total);
        }

        System.out.println(res);
    }
}