题目描述
动物王国中有三类动物 A,B,C,这三类动物的食物链构成了有趣的环形。
A 吃 B,B 吃 C,C 吃 A。
现有 N 个动物,以 1∼N 编号。
每个动物都是 A,B,C 中的一种,但是我们并不知道它到底是哪一种。
有人用两种说法对这 N 个动物所构成的食物链关系进行描述:
第一种说法是 1 X Y,表示 X 和 Y 是同类。
第二种说法是 2 X Y,表示 X 吃 Y。
此人对 N 个动物,用上述两种说法,一句接一句地说出 K 句话,这 K 句话有的是真的,有的是假的。
当一句话满足下列三条之一时,这句话就是假话,否则就是真话。
当前的话与前面的某些真的话冲突,就是假话;
当前的话中 X 或 Y 比 N 大,就是假话;
当前的话表示 X 吃 X,就是假话。
你的任务是根据给定的 N 和 K 句话,输出假话的总数。
输入格式
第一行是两个整数 N 和 K,以一个空格分隔。
以下 K 行每行是三个正整数 D,X,Y,两数之间用一个空格隔开,其中 D 表示说法的种类。
若 D=1,则表示 X 和 Y 是同类。
若 D=2,则表示 X 吃 Y。
输出格式
只有一个整数,表示假话的数目。
数据范围
1≤N≤50000,
0≤K≤100000
输入样例:
100 7
1 101 1
2 1 2
2 2 3
2 3 3
1 1 3
2 3 1
1 5 5
输出样例:
3
算法并查集
思路:
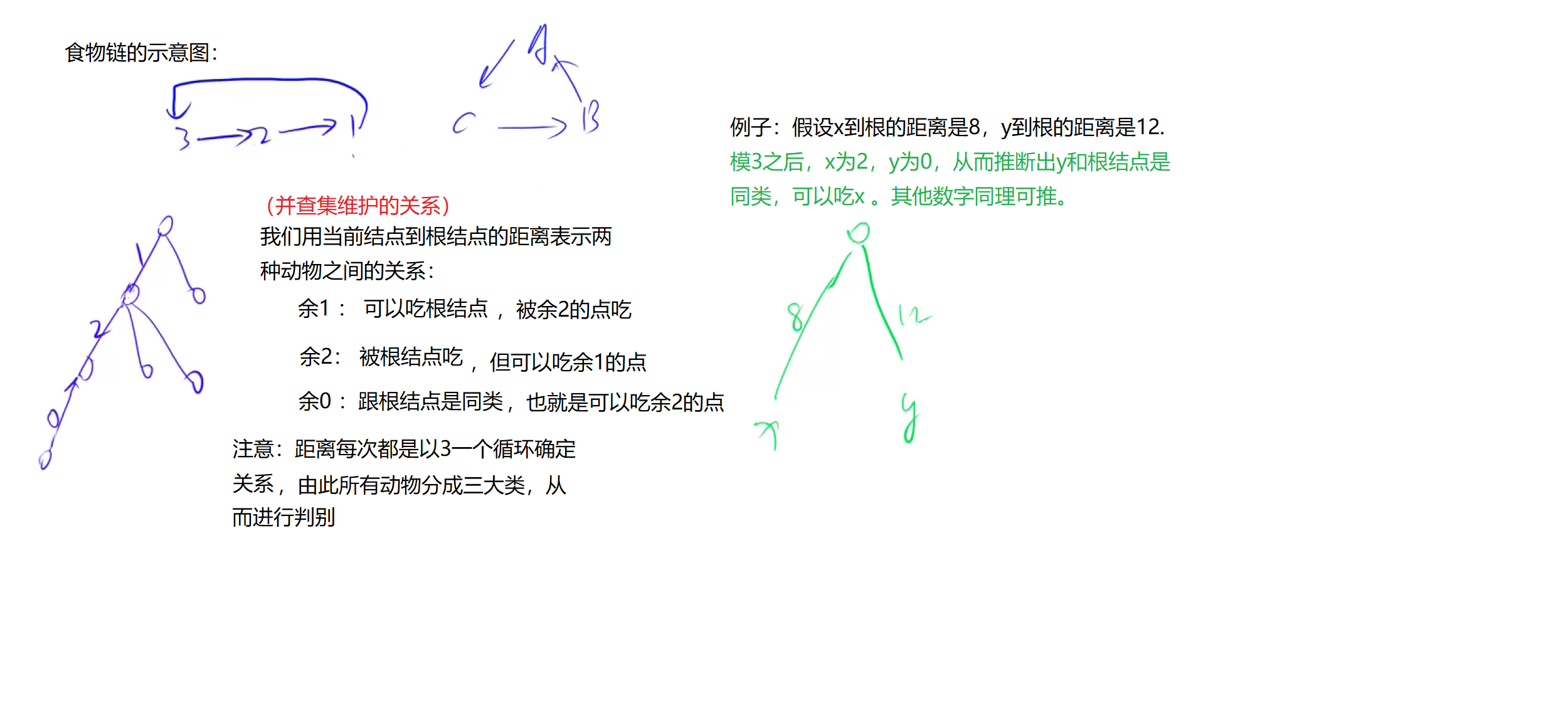
1. 用一个距离数组维护每个动物之间的关系,因为有三种关系,所以我们把每个结点到根结点之间的距离模3之后就会得到对应的关系,如:4%3=1,表示这个结点是可以吃根结点那个种类的动物。其他数字的情况类似,具体在下方图中。
2. 关系确定之后,那就剩下怎么把所有的动物都整合到一个集合中。并查集就是这个作用。
3. 我们会首先对假话的三种情况做判断,第一种x和y超出n的范围;第二种,t=1两个是同类;第三种,t=2,x吃y。
4. 在判断假话的时候x和y可能不在一个集合中,所以还会进行两个集合的合并。
(思路大概就是这样,详情看代码)
2022-4-4 :更新对于算法流程的解释,合并集合后距离数组更新的解释。(此次较为详细,也是为了避免以后复习麻烦)
参考文献
y总讲解视频
C++ 代码
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
//最多5w个点
const int N = 50010;
//p数组维护并查集的,含义:每个结点的根结点是谁 d数组维护每个结点到根结点的距离
int p[N] , d[N];
//n:有多少中动物 m:有多少句话
int n , m;
//并查集找结点的根结点的函数。这个函数就要对d数组进行一些维护更新
int find(int x){
//如果x不是树根
if(p[x] != x){
//先用一个变量存一下根结点是谁。
int t = find(p[x]);
/*d[x]到根节点的距离=d[x]到父结点的距离 +父结点到根结点的距离
p[x]find完之后,p[x]就等于根结点了,所以d[p[x]]存的就是p[x]到根结点
的距离
d[x] 存的是这个结点到他自己父结点的距离,所以写成下面那样。
*/
d[x] += d[p[x]];
//p[x]重新更新成t,直接指向根结点
p[x] = t;
}
return p[x];
}
int main(){
scanf("%d%d" , &n, &m);
//初始化
for(int i = 1 ; i <= n ; i++){
//首先自己是一个集合
p[i] = i;
//d数组是全局变量,所以初始化本来是0,如果定义的不是全局变量,那就要初始化一下
}
//res假话的个数
int res = 0 ;
while(m--){
//t表示说法的种类 x 和y表示不同或者相同的种类
int t , x , y ;
scanf("%d%d%d" , &t ,&x , &y);
//x或y大于n , 假话
if(x > n || y > n){
res++;
}else{//满足在(1,n)之间的这个范围
//先找出x , y的根结点
int px = find(x) , py = find(y);
if(t == 1){//t=1, x,y是同一类
//px=py判断x和y是不是在同一棵树上, 并且不是同一类 , 那就是假话
if(px == py && (d[x] - d[y]) % 3 != 0) res++;
else if(px != py){//x和y不在一个集合里面,就把他们进行合并
//把x的根结点找个父结点,即y的根结点,从而达成合并
p[px] = py;
/*合并后,更新x到新根结点的距离
x和y是同一个集合里面的,并且因为此时x和y是同一类,所以他们到根结点的距离一样。
因为x原来的根结点px到新根结点的距离 等于d[y] 等于 d[x] + d[px];所以推出下面这个式子。
*/
d[px] = d[y] - d[x];
}
}else{//t=2,x吃y,也就是说x在y结点的下面,模3情况下比y多1
/*px = py在同一个集合里面
dx是到根结点的距离,dy同理,因为x是吃y的,所以在模3的情况下,dx比dy多1
也就是说(dx - dy-1)%3 = 0。所以推出当(d[x] - d[y] - 1) %3 != 0的时候
就是一句假话。
*/
if(px ==py && (d[x] - d[y] - 1) %3 != 0) res++;
else if(px != py){//x和y不在一个集合里面,把他们进行合并
//和上面合并一样,也是把y的根结点变成x的根结点的父结点
p[px] = py;
//同时更新x原来的根结点px到新根结点(也就是py)的距离
d[px] = d[y] + 1 - d[x];
}
}
}
}
printf("%d\n" , res);
return 0;
}

