题目描述

给定一颗树，树中包含n个结点（编号1~n）和n-1条无向边。

请你找到树的重心，并输出将重心删除后，剩余各个连通块中点数的最大值。

重心定义：重心是指树中的一个结点，如果将这个点删除后，剩余各个连通块中点数的最大值最小，那么这个节点被称为树的重心。

输入格式
第一行包含整数n，表示树的结点数。

接下来n-1行，每行包含两个整数a和b，表示点a和点b之间存在一条边。

输出格式
输出一个整数m，表示将重心删除后，剩余各个连通块中点数的最大值。

数据范围
1≤n≤10^5

样例

输入样例
9
1 2
1 7
1 4
2 8
2 5
4 3
3 9
4 6
输出样例：
4

算法1

深度优先搜索

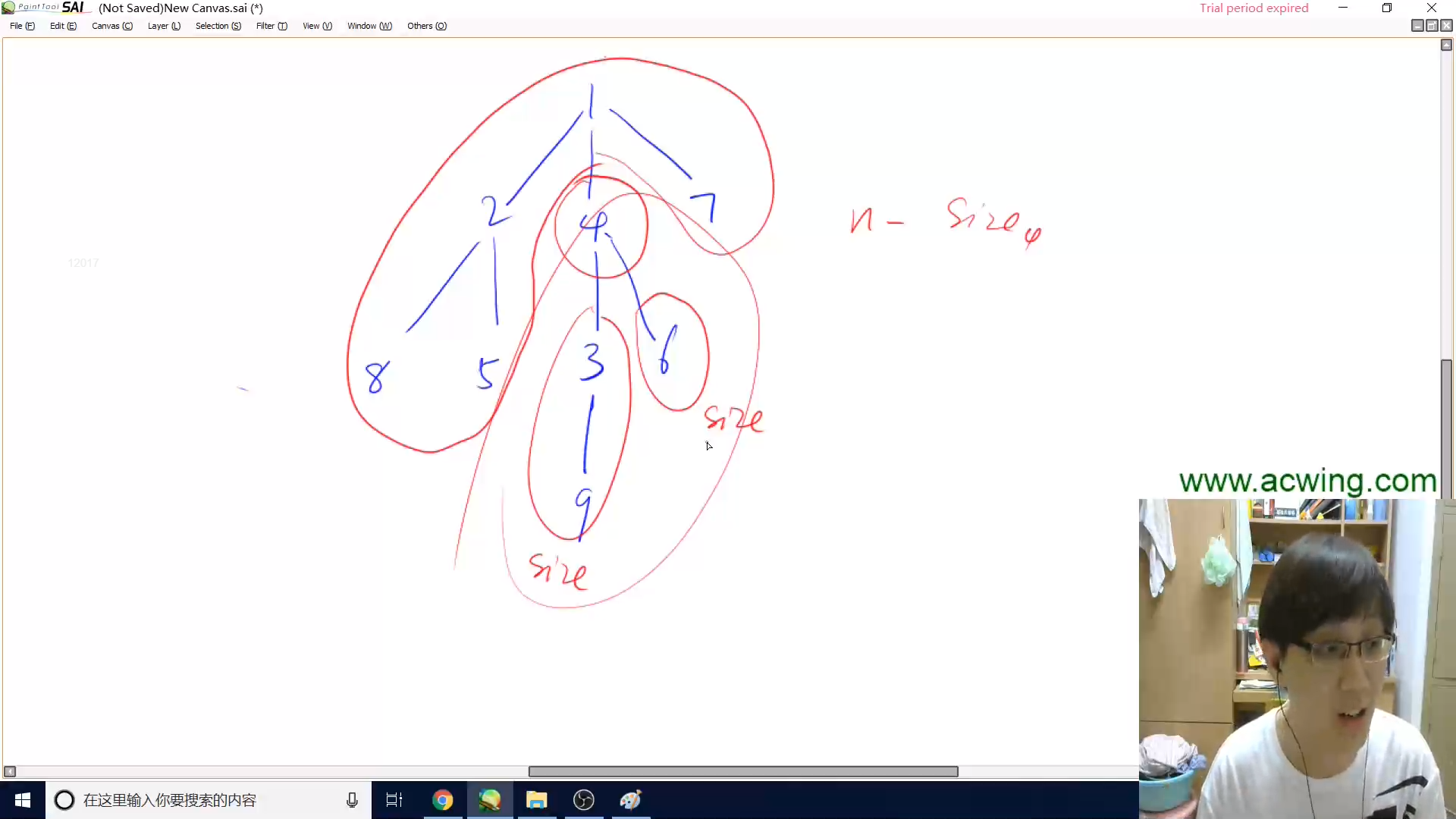
深度优先遍历，一种特殊的深搜
把每个点删除后的连通块的最大值求出来，输出其中最小的
时间复杂度，每个点都会只被遍历一次，O(m+n)

python 代码

def add(a,b):
    global idx
    e[idx] = b
    ne[idx] = h[a]
    h[a] = idx
    idx+=1

#返回以u为根的子树的点的数量
def dfs(u):
    global ans
    st[u]=True
    i=h[u]
    sum=1       #存储当前子树的大小
    res = 0     #把当前点删掉后每一个连通块大小的最大值
    while i!=-1:
        j=e[i]
        if st[j]==False:
            s=dfs(j)
            res=max(res,s)
            sum+=s
        i=ne[i]
    res = max(res,n-sum)
    ans = min(ans,res)
    return sum

if __name__ == "__main__":
    N = 100010
    M = N*2
    h = [-1]*N
    e = [0]*M
    ne = [0]*M
    st = [False]*N      #哪些点被搜过
    idx=0
    ans=N               #全局答案
    n = int(input())
    for i in range(n-1):
        a,b = map(int,input().split())
        add(a,b)
        add(b,a)
    dfs(1)

    print(ans)