背包问题：

• 01背包问题
• 完全背包问题
• 多重背包问题
• 分组背包问题

完全背包问题

问题描述:有$N$种物品和一个容量是$V$的背包，每种物品都有无限件可用,第$i$种物品的体积是$vi$，价值是 $wi$,求解将哪些物品装入背包，可使这些物品的总体积不超过背包容量，且总价值最大,输出最大价值。

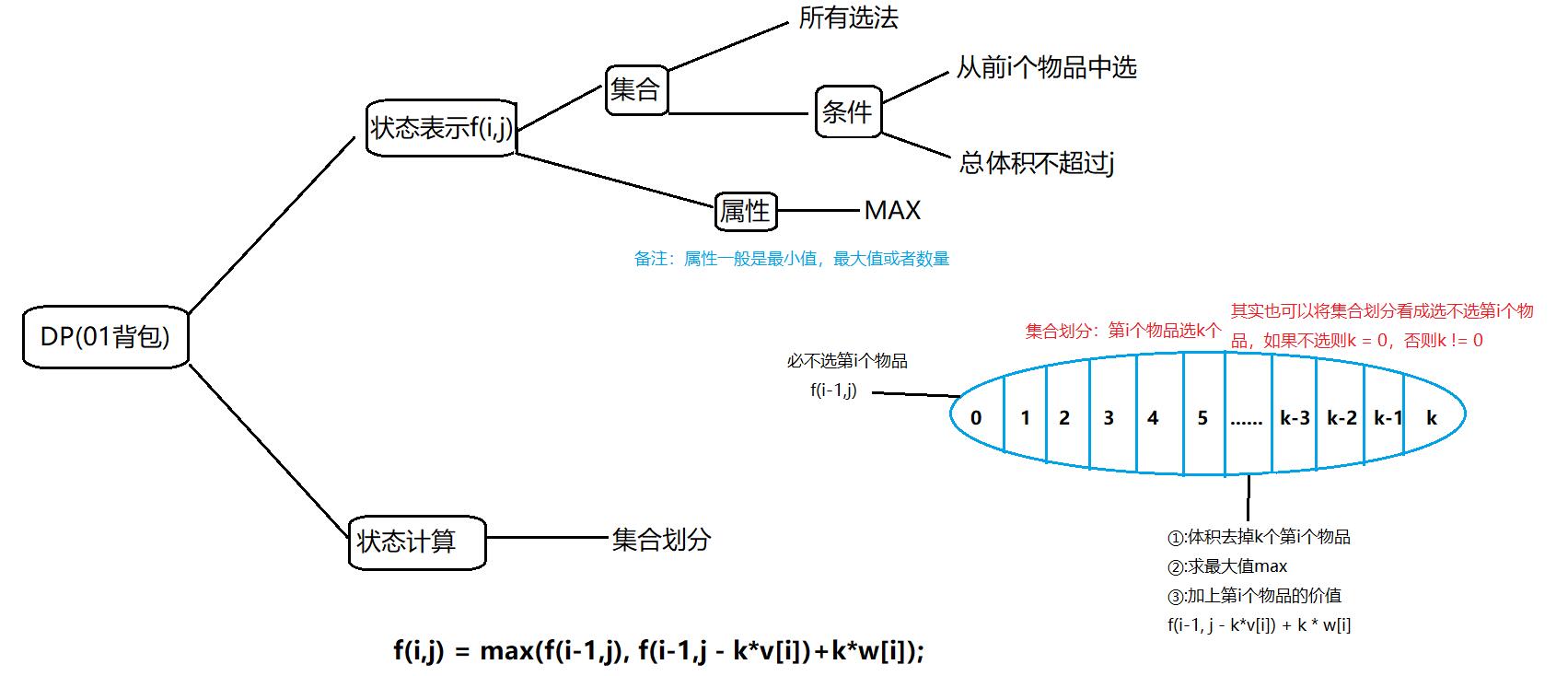
版本一(c++代码)：

#include <iostream>
#include <algorithm>

using namespace std;
const int N = 1010;

int v[N], w[N];
int f[N][N];
int n, m;

int main()
{
    cin >> n >> m;
    for(int i = 1;i <= n; i ++ ) cin >> v[i] >> w[i];

    for(int i = 1;i <= n; i ++ )
        for(int j = 0;j <= m; j ++ )
            //枚举第i个物品有k件
            for(int k = 0; k * v[i] <= j; k ++ )
                f[i][j] = max(f[i][j], f[i - 1][j - k*v[i]] + k*w[i]);

    cout << f[n][m] << endl;
    return 0;
}

版本一的是时间复杂度是$O(n^3)$ 考虑优化 $f(i-1, j - k*v) + k * w$ 展开来写:
$$f(i-1,j - v) + w , f(i-1,j - 2v) + 2w , f(i-1,j - 3v) + 3w,......f(i-1,j - kv) + kw$$
可以考虑去掉项使之变位二维 $f(i-1,j-v)$ 展开来写(按照上面的展开方式)
$$f(i-1,j-v),f(i-1,j-2v) + w,f(i-1,j-3v) + 2w,f(i-1,j-4v)+3w,......f(i-1,j-kv)+(k-1)w$$

可以看出 $f(i-1, j - k*v) + k * w == f(i-1,j-v) + w$
版本二(c++代码):

#include <iostream>
#include <algorithm>

using namespace std;
const int N = 1010;

int v[N], w[N];
int f[N][N];
int n, m;

int main()
{
    cin >> n >> m;
    for(int i = 1;i <= n; i ++ ) cin >> v[i] >> w[i];

    for(int i = 1;i <= n; i ++ )
        for(int j = 0;j <= m; j ++ )
        {
            f[i][j] = f[i-1][j];
            if(j >= v[i]) f[i][j] = max(f[i][j], f[i][j - v[i]] + w[i]);
        }

    cout << f[n][m] << endl;
    return 0;
}

再次优化：优化与01背包相似，可参考我的01背包优化过程
版本三(c++代码)：

#include <iostream>
#include <algorithm>

using namespace std;
const int N = 1010;

int v[N], w[N];
int f[N];
int n, m;

int main()
{
    cin >> n >> m;
    for(int i = 1;i <= n; i ++ ) cin >> v[i] >> w[i];

    for(int i = 1;i <= n; i ++ )
        for(int j = v[i];j <= m; j ++ )
            f[j] = max(f[j], f[j - v[i]] + w[i]);

    cout << f[m] << endl;
    return 0;
}