背包问题：

• 01背包问题
• 完全背包问题
• 多重背包问题
• 分组背包问题

01背包问题

问题描述:有$N$件物品和一个容量是$V$的背包。每件物品只能使用一次。第$i$件物品的体积是$vi$，价值是$wi$,求解将哪些物品装入背包，可使这些物品的总体积不超过背包容量，且总价值最大,输出最大价值。

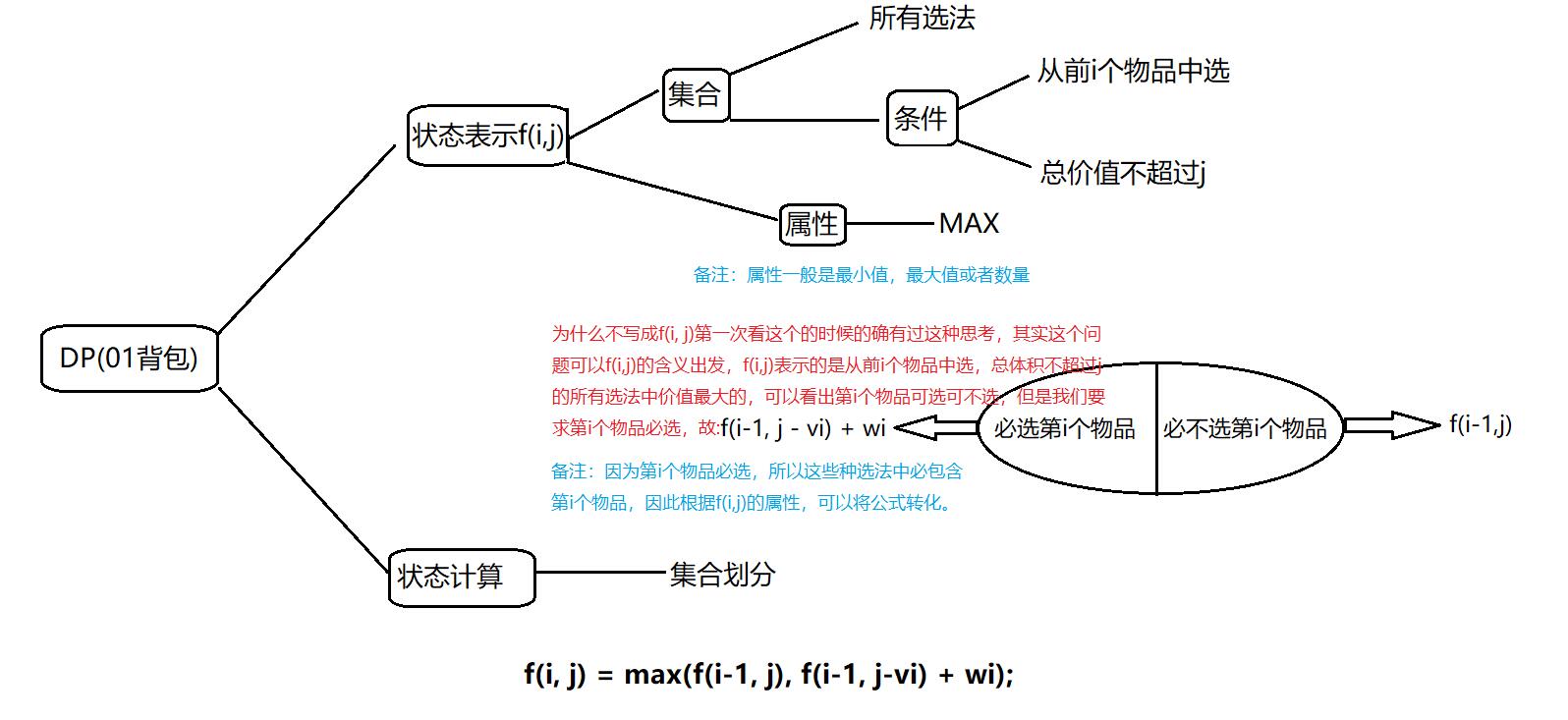
未优化c++代码：

#include <iostream>
#include <algorithm>

using namespace std;
const int N = 1010;

int v[N],w[N];
int f[N][N];
int n, m;

int main()
{
    cin >> n >> m;
    //为什么从1开始输入:f[0][0~m] == 0 不用处理
    for(int i = 1; i <= n; i ++ ) cin >> v[i] >> w[i];
    for(int i = 1; i <= n; i ++ )
    {
        for(int j = 0;j <= m; j ++ )
        {
            f[i][j] = f[i-1][j];
            if(j >= v[i]) f[i][j] = max(f[i][j], f[i - 1][j - v[i]] + w[i]); 
        }
    }
    cout << f[n][m] << endl;
    return 0;
}

优化c++代码

#include <iostream>
#include <algorithm>

using namespace std;
const int N = 1010;

int v[N],w[N];
//优化:拿掉[i] 
//因为我们只用到了f[i-1] 所以进入循环后f[i] = f[i - 1] 上一层循环的i刚好是i-1
int f[N];
int n, m;

int main()
{
    cin >> n >> m;
    //为什么从1开始输入:f[0][0~m] == 0 不用处理
    for(int i = 1; i <= n; i ++ ) cin >> v[i] >> w[i];
    for(int i = 1; i <= n; i ++ )
    {
        /*为什么逆序：
          正序：f[i][大]由f[i-1][小]更新 如果不逆序f[i-1][小]已经被更新成了f[i][小]
          逆序：f[i][大]由f[i-1][小]更新 逆序f[i][小]在第i轮还没有被计算仍为f[i-1][小]
        */
        for(int j = m;j >= v[i]; j -- )
        {
            //f[i][j] = f[i-1][j]; 优化前
            //if(j >= v[i]) f[i][j] = max(f[i][j], f[i - 1][j - v[i]] + w[i]);
            f[j] = max(f[j], f[j - v[i]] + w[i]);
        }
    }

    //f[n][j] == f[j] 等价
    cout << f[m] << endl;
    return 0;
}