双栈+操作符优先级实现 时间复杂度$O(len(s))$

双栈：运算符栈和操作数栈
那么操作符优先级怎么定义呢？
优先级分为栈内优先级（in stack priority）isp 和 栈外优先级（in coming priority）icp
isp[op]表示该操作符op在栈内的优先数, icp[op]表示该操作符op在栈外的优先数,对于isp和icp可以用一个map存储$char$ 到 $int$ 的映射

isp, icp的取值注意点

1. 对于+ 或 - 的优先数相等, * 或 / 的优先数相等
2. 对于同一个操作符op, isp[op] > icp[op]
3. */ 大于 +-

#include<iostream>
#include<map>
#include<stack>
using namespace std;
map<char, int> isp, icp;
const char opers[6] = {'+', '-', '*', '/', '(', ')'};
const int isps[6] = {3, 3, 5, 5, 1, 6}, icps[6] = {2, 2, 4, 4, 6, 1};
void init() {
    for(int i = 0; i < 6; ++i) isp[opers[i]] = isps[i], icp[opers[i]] = icps[i];
}

void calc(stack<char>& ops, stack<int>& nums) {
    int b = nums.top(); nums.pop();
    int a = nums.top(); nums.pop();
    char op = ops.top(); ops.pop();
    int t;
    if(op == '+') t = a + b;
    else if(op == '-') t = a - b;
    else if(op == '*') t = a * b;
    else t = a / b;
    nums.push(t);
}

int calculate(string s) {
    s = "(" + s + ")";
    stack<char> ops;
    stack<int>  nums;
    int n = s.size();
    for(int i = 0; i < n; ++i) {
        if('0' <= s[i] && s[i] <= '9') {
            int t = s[i] - '0';
            for(int j = i + 1; j < n; ++j) {
                if('0' <= s[j] && s[j] <= '9') t = t * 10 + (s[j] - '0');
                else {
                    i = j - 1;
                    nums.push(t);
                    break;
                }
            }
        } else if(s[i] == ' ') continue;
        else {
            if(ops.empty() || isp[ops.top()] < icp[s[i]]) ops.push(s[i]);
            else if(isp[ops.top()] == icp[s[i]]) ops.pop();
            else {
                calc(ops, nums);
                i--;
            }
        }
    }
    return nums.top();
}

int main() {
    init();
    string s;
    cin >> s;
    cout << calculate(s);
    return 0;
}

几个小技巧

1. 将s用()括起来（即s = “(” + s + “)”）
   当s = “1 + 2” 时，如果不在后面加上
   while(ops.size()) calc(ops, nums);
   ，会WA，s加上括号可以强制使操作符栈的操作符计算完
2. 在 calc中输出 a b op 可以得到后缀表达式(注意不要将计算后的值加入后缀表达式)

附

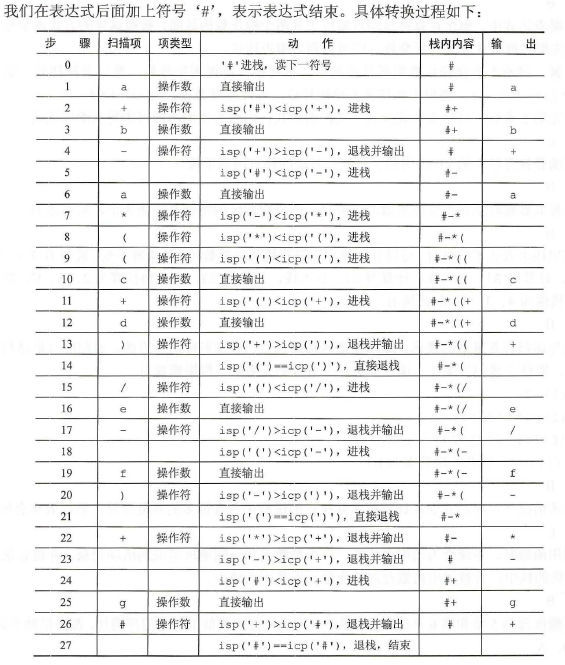
a+b-a*((c+d)/e-f)+g