分析

$f[u][p]：包含节点u,选择了p个节点的距离最小值 $

$ f[u][p]=min\(f[u][p],f[u][p-q]+f[v][q]+w\*\(K-q\)\*q\) $

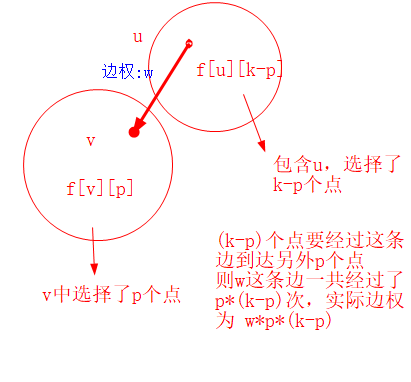
当前一共选择了p个点，包含v的节点中选择了q个点，包含u的节点中选择了p-q个点，当前的权值为w的边一共经过了$q\*\( p-q)$次 (两边每个点两两之间都要经过这条边)，实际权值为$w\*q*(p-q)$

C++ 代码

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 5e4+10;
int n,m,K,siz[N];
int h[N],e[2*N],w[2*N],ne[2*N],idx;
LL f[N][110];
unordered_map<int,int> mp;  //哈希表，记录是否为重要节点
void add(int a,int b,int c)
{
    e[idx]=b,w[idx]=c,ne[idx]=h[a],h[a]=idx++;
}
void dfs(int u,int father)
{
    f[u][0]=0;      //在包含u这棵子树中选0个点，最小距离为0
    if(mp[u]) siz[u]=1,f[u][1]=0;   //u是重要节点，包含u的重要节点集合大小为1。 在包含u的这棵子树中选择一个节点(u自己)，最小距离为0 (我到我自己)
    for(int i=h[u];~i;i=ne[i])  
    {
        int j=e[i];
        if(j==father) continue;   //当前点j为其父亲节点，跳过
        dfs(j,u);   //搜索u的子节点j的情况
        siz[u]+=siz[j];     //u集合的大小+j集合的大小
        for(int p=min(K,siz[u]);p>=0;p--)   //当前一共选了p个点，最多选取K个节点，两者间取最小值
            for(int q=0;q<=min(p,siz[j]);q++)    //在j中选择的节点数为当前已选节点数p和siz[j]的最小值
                //包含u的子树，选取p个节点的最小值为min(f[u][p],包含子节点j,选择了p-q个节点的最小值+包含子节点j，选择了q个节点的最小值+实际边权值)
                f[u][p] = min(f[u][p], f[u][p-q]+f[j][q]+(LL)w[i]*(K-q)*q); 
    }   
}
int main()
{
    memset(h,-1,sizeof h);
    scanf("%d%d%d",&n,&m,&K);
    int x,a,b,c;
    for(int i=0;i<m;i++)
    {
        scanf("%d",&x); mp[x]=1;
    }
    for(int i=0;i<n-1;i++)
    {
        scanf("%d%d%d",&a,&b,&c);
        add(a,b,c),add(b,a,c);
    }
    memset(f,0x3f,sizeof f);    //求最小值，初始化为最大值
    dfs(1,-1);  //设1为根节点，父亲节点为-1，从1开始进行dfs
    cout<<f[1][K];  //包含根节点1，选择了K个节点的集合的距离最小值

    return 0;
}