@TOC

剑指 Offer 53 - II. 0～n-1中缺失的数字

一个长度为n-1的递增排序数组中的所有数字都是唯一的，并且每个数字都在范围0～n-1之内。在范围0～n-1内的n个数字中有且只有一个数字不在该数组中，请找出这个数字。

示例 1:

输入: [0,1,3]
输出: 2

示例 2:

输入: [0,1,2,3,4,5,6,7,9]
输出: 8

限制：

• 1 <= 数组长度 <= 10000

解法一：下标对应法

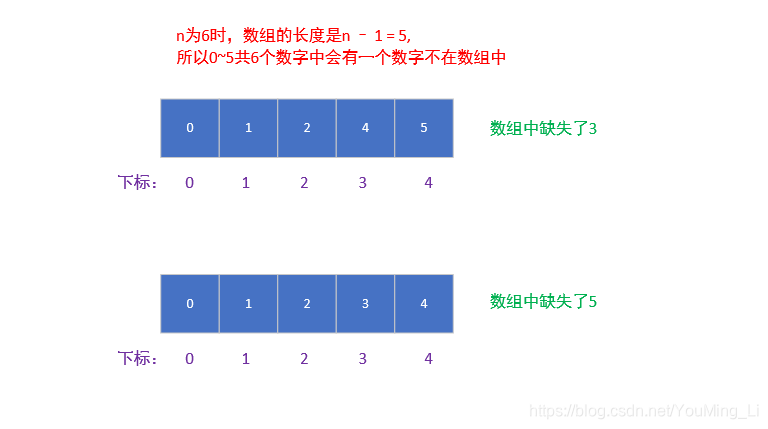
数组长度n-1,元素范围0 ~ n-1,共n个数，如果数组长度是n的话，也即所有数都出现一次，那么排序后，数组中当前元素的值应该和其所在索引相同，我们找到第一个不同的，下标代表的就是缺失的数。

要注意的是当所有的nums[i] = i时，缺失的就是最后一个n-1,即nums.length。

时间复杂度： $O(n)$

Java代码

class Solution {
    public int missingNumber(int[] nums) {
        for(int i = 0;i < nums.length;i++){
            if(nums[i] != i){
                return i;
            }
        }
        return nums.length;
    }
}

解法二：二分

这道题目给定的是递增数组，假设数组中第一个缺失的数是 x，那么数组中的数如下所示；

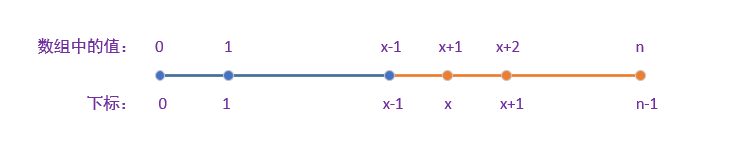
从中可以看出，数组左边蓝色部分都满足nums[i] == i，数组右边橙色部分都不满足nums[i] == i，满足了二分法中的二段性质，因此我们可以二分找出不满足nums[i] = i的左边界。

另外同解法一，要注意特殊情况：当所有数都满足nums[i] == i时，表示缺失的是 n。

时间复杂度： 二分中的迭代只会执行 $O(logn)$次，因此时间复杂度是 $O(logn)$。

Java代码

class Solution {
    public int missingNumber(int[] nums) {
        //二分，找到不满足nums[i] == i的左边界
        //要注意的是当所有的nums[i]=i时，缺失的就是最后一个n-1,即nums.length
        int l = 0,r = nums.length - 1;
        while(l < r){
            int mid = l + r >> 1;
            if(nums[mid] != mid ) r = mid;
            else l = mid + 1; 
        }

        if(nums[r] == r) return nums.length;
        else return r;
    }
}