题目描述

有 N 件物品和一个容量是 V 的背包。每件物品只能使用一次。

第 i 件物品的体积是 vi，价值是 wi。

求解将哪些物品装入背包，可使这些物品的总体积不超过背包容量，且总价值最大。
输出最大价值。

输入格式
第一行两个整数，N，V，用空格隔开，分别表示物品数量和背包容积。

接下来有 N 行，每行两个整数 vi,wi，用空格隔开，分别表示第 i 件物品的体积和价值。

输出格式
输出一个整数，表示最大价值。

数据范围
0<N,V≤1000
0<vi,wi≤1000

样例

输入样例
4 5
1 2
2 4
3 4
4 5
输出样例：
8

算法1

dp

f[i][j],表示只看前i个物品，总体积是j的情况下总价值最大是多少
f[i][j]
1.不选第i个物品f[i][j] = f[i-1][j] 总体积不超过j的情况下，前i-1个物品的最大价值
2.选第i个物品f[i][j] = f[i-1][j-v[i]] 第i个物品已经考虑完了，所以只考虑i-1，因为选了第i个物品后的体积是j，所以考虑前i个物品的体积是j-v[i]
f[i][j] = max{1. 2.}
初始化f[0][0] = 0

闫氏dp分析法：
1.状态表示
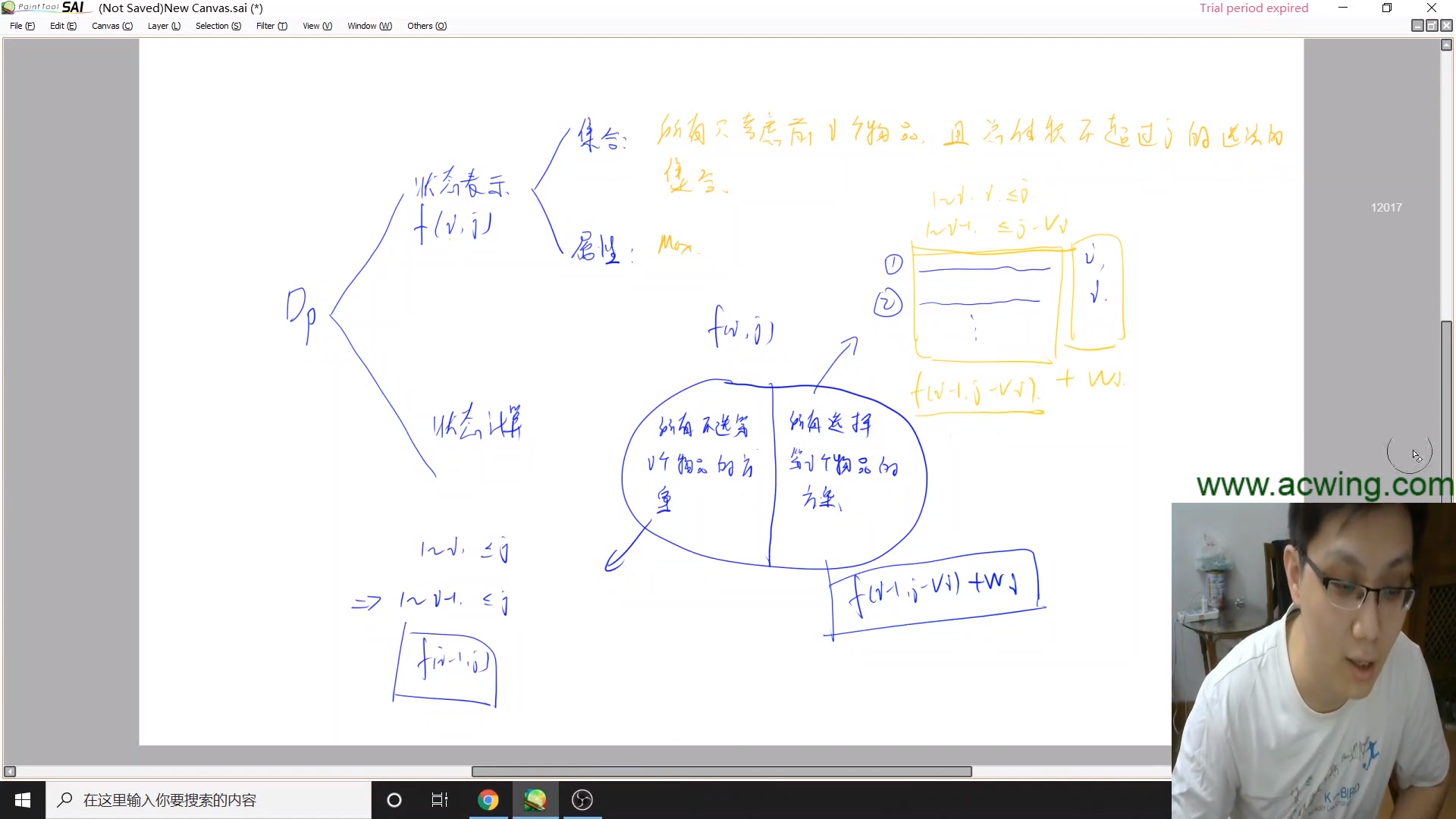
集合：所有只考虑前i个物品，并且总体积不超过j的选法的集合
属性：max
2.状态计算
f[i][j]表示集合中的最大值
f[i][j]先划分子集
f[i][j] 选第i个或不选第i个。
不选第i个，f[i-1][j],选第i个，第i个一定要选，前i-1个不一定，f[i-1][v-vi]+wi,f[i][j]=max(f[i-1][j],f[i-1][v-vi]+wi)

python代码,朴素写法

if __name__ == "__main__":
    n,m = map(int,input().split())
    N = 1010
    f = [[0] * N for _ in range(N)]
    v = [0] * N         #体积
    w = [0] * N         #价值
    for i in range(1,n+1):
        v[i],w[i] = map(int,input().split())
    for i in range(1,n+1):
        for j in range(0,m+1):
            f[i][j] = f[i-1][j]         #左半边子集
            if j>=v[i]:
                f[i][j] = max(f[i-1][j],f[i-1][j-v[i]]+w[i])

    print(f[n][m])

python代码,空间优化写法

优化，因为第一维只用到f[i]和f[i-1]，因此用滚动数组，只保留上一次的值。
把第一维去掉,f[i][j]=max(f][j],[v-vi]+wi)，从大到小循环，两方程等价。
逆序遍历的是j，
正常情况下用第i-1层来更新第i层，若用正序，f[j]会被第i层更新的值覆盖掉，就会变成用第i层来更新第i层，显然是错的。

if __name__ == "__main__":
    n,m = map(int,input().split())
    N = 1010
    f = [0] * N
    v = [0] * N         #体积
    w = [0] * N         #价值
    for i in range(1,n+1):
        v[i],w[i] = map(int,input().split())
    for i in range(1,n+1):
        for j in range(m,v[i]-1,-1):        #j表示从m递减到v[i]
            if j>=v[i]:                 
                f[j] = max(f[j],f[j-v[i]]+w[i])
    print(f[m])