@TOC

剑指 Offer 51. 数组中的逆序对

在数组中的两个数字，如果前面一个数字大于后面的数字，则这两个数字组成一个逆序对。输入一个数组，求出这个数组中的逆序对的总数。

示例 1:

输入: [7,5,6,4]
输出: 5

限制：

• 0 <= 数组长度 <= 50000

解题思路

记住一句话，求逆序对是归并排序的典型应用之一。那我们看完题目就知道这题肯定是用归并排序了。

归并排序是利用归并的思想实现排序的方法，该算法的核心就是分治策略，即分与治。
- 分：将问题分成小的问题然后递归求解
- 治：将分阶段得到的各答案“修补”到一起，即分而治之。

下面就是用归并排序对[8,4,5,7,1,3,6,2]进行排序的示意图。

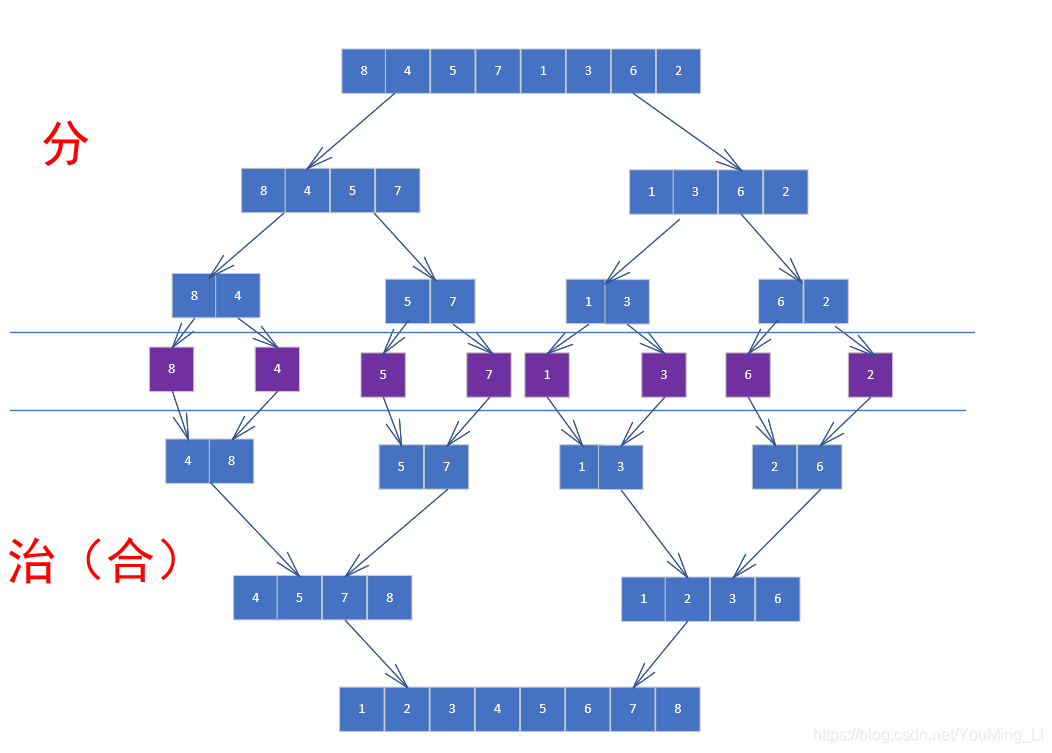
总结一下归并排序的思路：
1. 将当前区间分为两半[l,r] => [l,mid] [mid+1,r]
2. 开辟两个新的运行栈，递归排序左右两半
3. 归并，将左右两个有序序列合并成一个有序序列，返回上一级运行栈

回顾了一下归并排序之后，我们要如何用它来求解逆序对的问题呢？

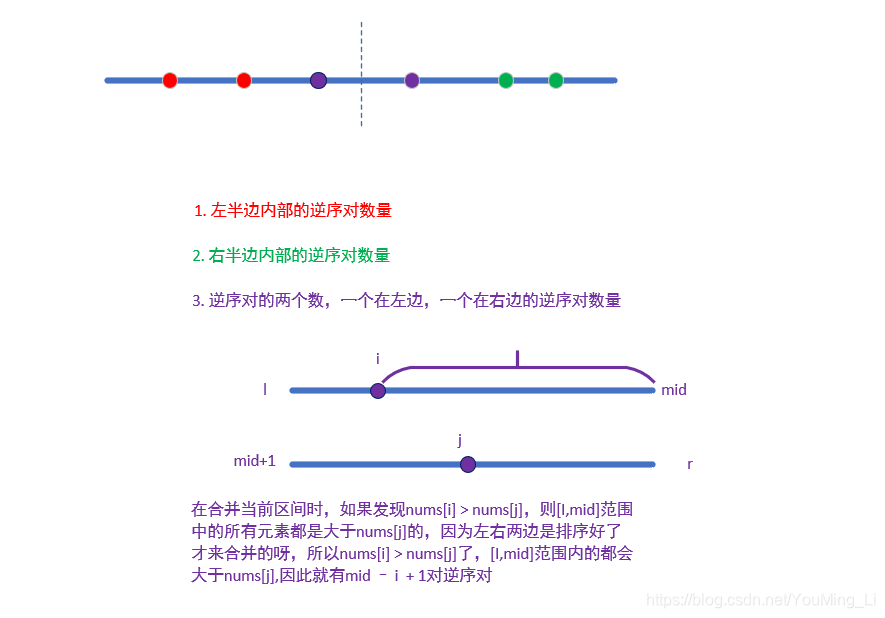
Java代码

class Solution {
    public int reversePairs(int[] nums) {
        //利用归并排序，总逆序对 = 左边逆序对 + 右边逆序对  + 逆序的两个数字分别在左右两边的逆序对
        if(nums == null || nums.length == 0) return 0;
        int[] temp = new int[nums.length];
        return mergeSort(nums,0,nums.length - 1,temp);

    }

    //分
    private int mergeSort(int[] nums,int l,int r,int[] temp){
        if(l >= r) return 0;//实际结束时，一定是l==r,即只有一个数了
        int mid = l + r >> 1;
        int left = mergeSort(nums,l,mid,temp);
        int right = mergeSort(nums,mid + 1,r,temp);
        int m = merge(nums,l,r,temp);
        return left + right + m;
    }

    //合
    private int merge(int[] nums,int l,int r,int[] temp){
        int mid = l + r >> 1;
        int k = l;
        int m = 0;
        int i = l,j = mid + 1;
        while(i <= mid && j <= r){
            if(nums[i] <= nums[j]){
                temp[k++] = nums[i++];
            }else{
                temp[k++] = nums[j++];
                m += (mid - i + 1);//nums[i]~nums[mid]均与nums[j]构成了逆序对，共mid-i+1对
            }
        }
        //扫尾,下面两个while循环同一轮只会执行其中一个，即其中一边还没有遍历结束的会执行扫尾
        while( i <= mid) temp[k++] = nums[i++];
        while( j <= r) temp[k++] = nums[j++];

        //将本次合并排序后的数放回原数组[l,r]的位置去
        i = l;
        k = l;
        while(i <= r){
            nums[i++] = temp[k++];
        }
        return m;
    }
}