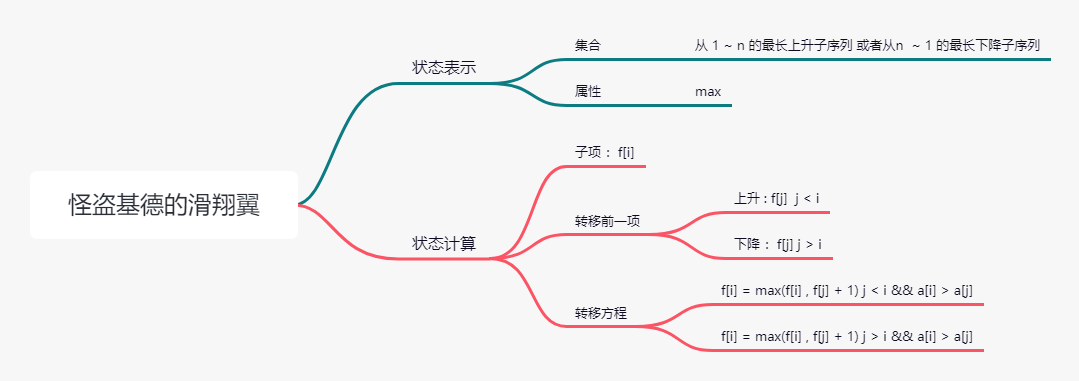
闫式dp分析法

/*

    分析  ： 
        1) 集合划分 1 3 2 5 4
        2)  转移
             2-1）如果 i > j 那么证明以i为结尾的序列可以继承j的上升序列 所以 f[i] = f[j] + 1 
             2-2) 如果 i < j 那么代表他不能继承他的序列，但是在1 ~ j 之间可能有序列可以被i继承 

        3) 结果 if a[i] > a[j]  
                    f[i] = max(f[i] , f[j] + 1);      

        4) 最后只需要比较一下f[i] 的最长上升子序列和最长下降子序列谁length就能解决该问题

*/




#include <iostream>
#include <algorithm>
#include <cstring>

using namespace std;

const int N = 110;

int h[N];
int f[N];

int k ;
int main() {

    cin >> k;
    while (k -- ) {

        int n ;
        cin >> n;memset(h , 0 , sizeof h);

        memset(f , 0 , sizeof f);
        for (int i = 1 ; i <= n ; i ++ ) cin >> h[i];

        int res = 0;
        for (int i = 1 ; i <= n ; i ++ ) {
            f[i] = 1;
            for (int j = 1 ; j < i ; j ++ ) {
                if (h[i] > h[j]) f[i] = max(f[i] , f[j] + 1);
                res = max(f[i] , res);
            }
        }
        memset(f , 0 , sizeof f);
        for (int i = n ; i >= 1 ; i -- ) {
            f[i] = 1;
            for (int j = n ; j > i ; j -- ) {
                if (h[i] > h[j]) f[i] = max(f[i] , f[j] + 1);
                res = max(f[i] , res);
            }
        }
        cout << res << endl;
    }

}