闫式dp分析法

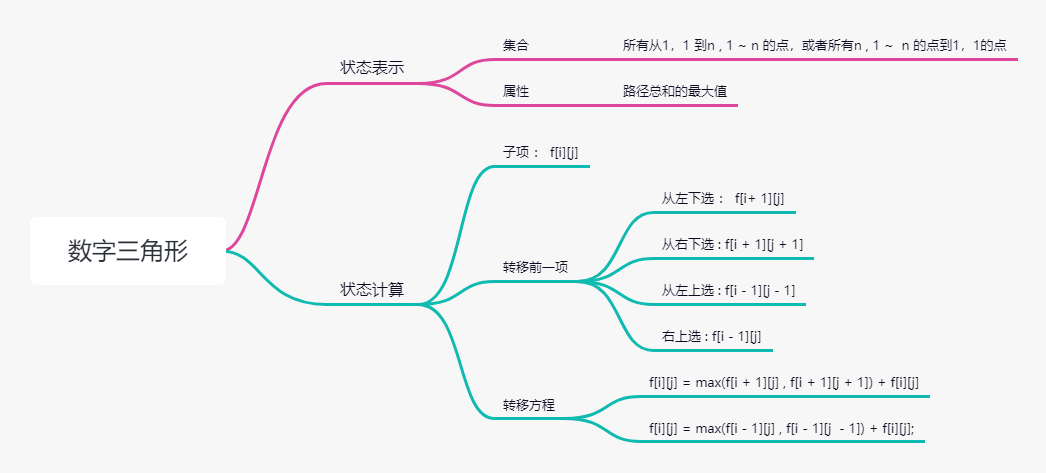
自上而下

import java.util.*;

public class Main {
    static int N = 510;
    static int[][] a = new int[N][N];
    static int[][] f = new int[N][N];

    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int n = sc.nextInt();
        for (int i = 1 ; i <= n ; i ++ ) {
            for (int j =1 ; j <= i ; j ++ ) a[i][j] = sc.nextInt();
        }

        for (int i = 1 ; i <= n ; i ++ ) {
            for (int j = 0 ; j <= i + 1 ; j ++ ) f[i][j] = Integer.MIN_VALUE; // 初始化节点为-03f3f3f3f
        }

        f[1][1] = a[1][1];
        for (int i = 2 ; i <= n ; i ++ ) {
            for (int j = 1 ; j <= i ; j ++ ) {
                f[i][j] = a[i][j] + Math.max(f[i - 1][j - 1] , f[i - 1][j]);
            }
        }
        int res = Integer.MIN_VALUE;
        for (int i = 1 ; i <= n ; i ++ ) res = Math.max(res , f[n][i]);

        System.out.println(res);

    }
}

自下而上，不用考虑边界问题

#include<bits/stdc++.h>
using namespace std;

const int N=510;
int f[N][N];
int n;

int main(){
    cin>>n;
    for(int i=1;i<=n;i++){
        for(int j=1;j<=i;j++){
            cin>>f[i][j];
        }
    }

    for(int i=n;i>=1;i--){
        for(int j=i;j>=1;j--){
            f[i][j]=max(f[i+1][j],f[i+1][j+1])+f[i][j];
        }
    }
    cout<<f[1][1]<<endl;
}