题目描述

原题

在给定的 N 个整数 A1，A2……AN 中选出两个进行 xor（异或）运算，得到的结果最大是多少？

输入格式
第一行输入一个整数 N。

第二行输入 N 个整数 A1～AN。

输出格式
输出一个整数表示答案。

数据范围
1≤N≤105,
0≤Ai<231

输入样例：
3
1 2 3
输出样例：
3

算法 Trie树

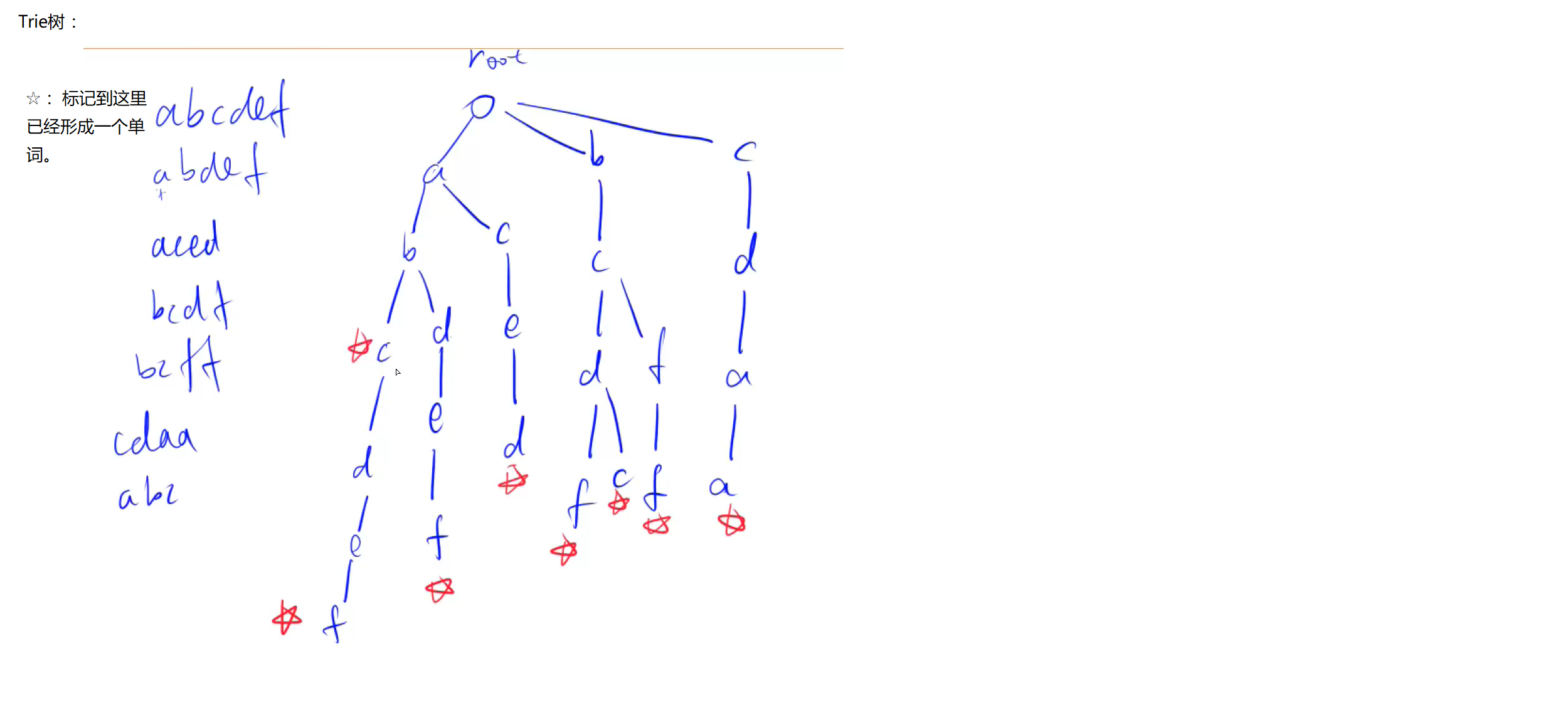
1. 先建立一个Trie树，根据题目给定的意思。

2. 然后对于当前遍历到的这个元素，我们查找与当前元素相同位上不同的数（因为每一个数都是用31位2进制来表示的，如果要异或之后是最大值，那么必须两个数的每一个位上都是不同的，一边1一边0，这样运算之后才会是最大的）。

3. 第二步中遍历树的时候，首先尽量保持当前位不同，如果没有不同的数，那么就再去看相同的数，如果还没有 这个分支，那就往上找。

参考文献

y总讲解视频

C++ 代码

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;
//N最多有多少个数  M:最多有多少个结点个数，最多有10w个数，每个数最多有31的长度,一个结点只能表示一位
const int N = 100010 , M = 3000000;//所以M是300w
//n多少个数
int n;
//定义tire树  idx 存储当前正在使用的下标
int son[M][2] , idx ;
//存放数的数组
int a[N];

/*往树中插入值
把每一个数看做一个31位长度的二进制数
*/
void insert(int x){
    //从根节点开始
    int p = 0;
    //i >= 0 等价 ~i（取反，因为-1在二进制中1111，取反后是0）.i从30最高位开始遍历
    for(int i = 30 ; ~i ; i--){
        /*x >> i & 1 : 意思就是说看一下x的二进制第i位是0还是1。
        这里的&不是去地址，而是引用！！
        */
        int &s = son[p][x >> i & 1 ];
        //如果不存在这个点
        if(!s) s = ++idx; //创建一个新结点
        //指向新的结点
        p = s;
    }
}

//查询
int query(int x){
    //res记录一个答案   p 在树上遍历的一个指针，一开始指向根结点0
    int res = 0 , p = 0;
    for(int i = 30 ; ~i ; i--){
        //这里和上面的意思一样：看一下x的二进制第i位是0还是1
        int s = x >> i & 1;
        //先看一下和当前这个点不一样的分支是否存在
        if(son[p][!s]){
            /*当前这一位是不一样的，所以这一位在当前的答案里面可以贡献一个多少位
              因为已经右移一位了，所以记录的时候要左移回去。
            */
            res += 1 << i;
            //如果存在，p就走到这个存在点的分支上
            p = son[p][!s];
        }else{//否则只能往相同的分支走
            p = son[p][s];
        }
    }
    return res;
}

int main(){
    cin>>n;
    for(int i = 0 ;i < n ;i++){
        cin>>a[i];
        //输入完数之后，建立索引
        insert(a[i]);
    }

    //定义答案
    int res = 0; 
    //枚举每个数异或之后最大值结果
    for(int i = 0 ; i < n ;i++) res = max(res ,query(a[i]));

    cout<<res <<endl;
    return 0;

}