闫式dp分析法

/*
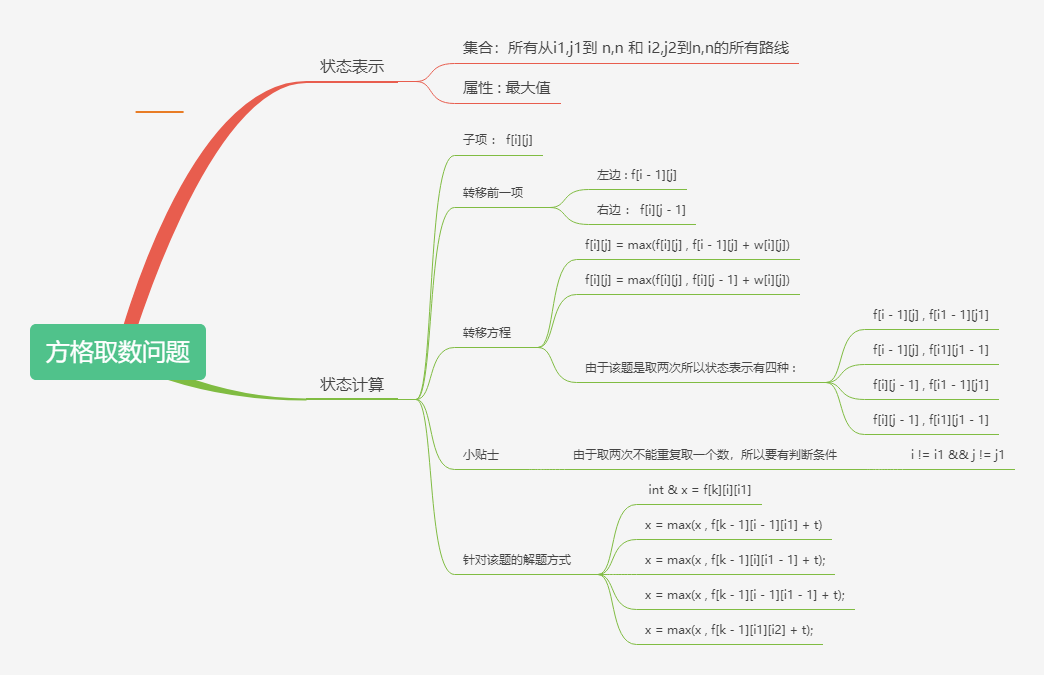
 1 . 由于是两次取数，那么我首先想到得是两次dp得方法。
 但是考虑到第一次dp无法记录是否选取所以采取了 f[i1][j1][i2][j2] 看作是(1 , 1) , (1 , 1) 到(n , n) , (n , n)。

 那么 i1 + j1 , i2 + j2 可以看作是 k    i1 + j1 == k , i2 + j2 == k 。 k = n * 2;

 2. 当 i1 = k - j1 , i2 = k - j2 且  i1 != i2 那么才不会重合
*/

#include <iostream>
#include <algorithm>
#include <cstring>

using namespace std;

const int N = 11;

int g[N][N];
int f[N * 2][N][N];

int n ;

int main() {

    cin >> n;
    int x , y , c;
    while (cin >> x >> y >> c , x && y && c) g[x][y] = c;

    for (int k = 2 ; k <= n * 2 ; k ++ ) {
        for (int i1 = 1 ; i1 <= n ; i1 ++ ) {
            for (int i2 = 1 ; i2 <= n ; i2 ++ ) {
                int j1 = k - i1 , j2 = k - i2;
                if (j1 >= 1 && j1 <= n && j2 >= 1 && j2 <= n ) {
                    int t = g[i1][j1];
                    if (i1 != i2) t += g[i2][j2];
                    int &x = f[k][i1][i2];
                    x = max(x , f[k-1][i1-1][i2-1] + t);
                    x = max(x , f[k-1][i1-1][i2] + t);
                    x = max(x , f[k-1][i1][i2-1] + t);
                  / x = max(x , f[k-1][i1][i2] + t);
                }
            }
        }
    }
    cout << f[n * 2][n][n] << endl;
     return 0;
}