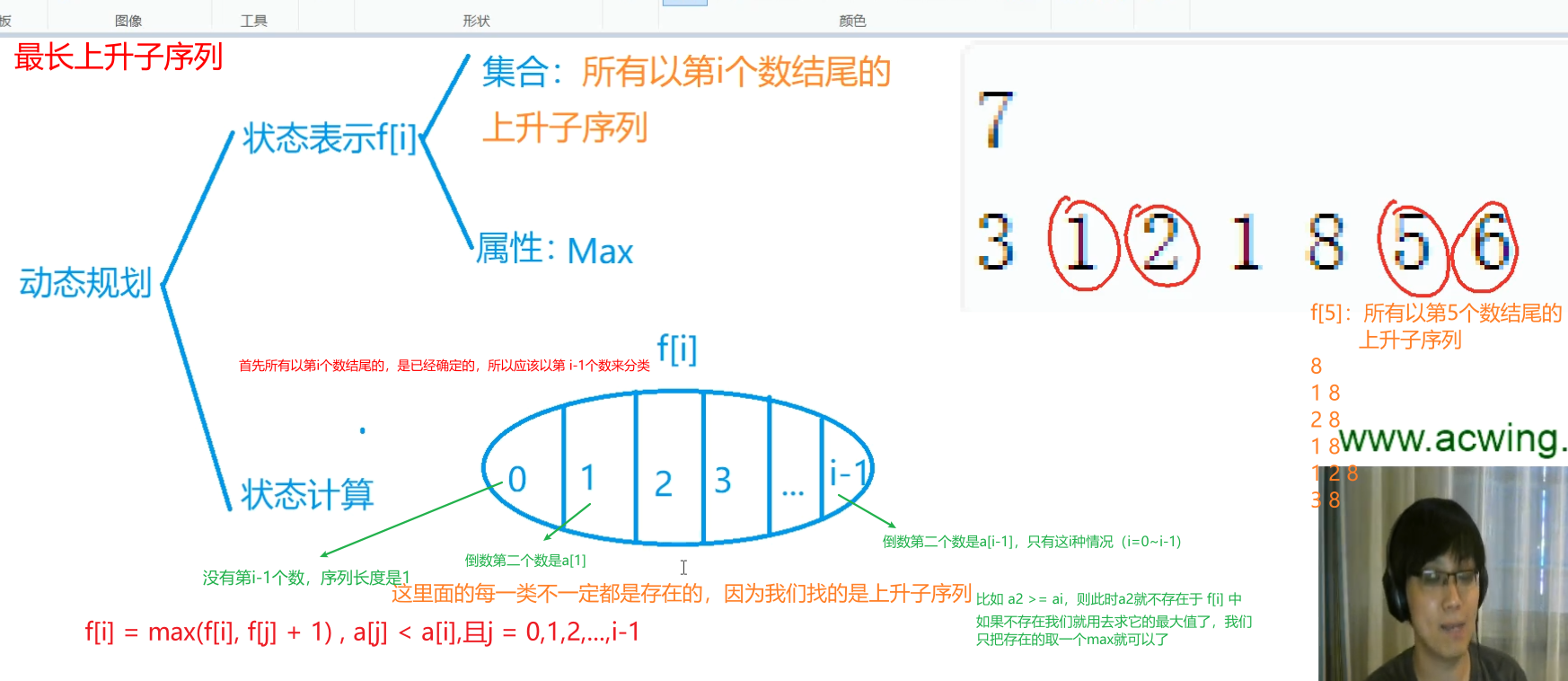
优化后的最长上升子序列代码：（1<=N<=1000）$O(N^2)$

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 1010;
int n;
int a[N];
int f[N];

int main (){
    cin >> n;
    for (int i = 0; i < n; i ++) cin >> a[i];

    for (int i = 0; i < n; i ++) {
        f[i] = 1; //f[i]设为默认是1，找不到前面数字小于自己的时候就为1
        for (int j = 0; j < i; j ++) // 否则枚举a[i]前一个数(j<i)是哪一个数，从1开始枚举 
            if (a[j] < a[i]) //满足这个条件才可以做     (易错！！！)
                f[i] = max(f[i], f[j] + 1);
    }

    int res = 0;
    for (int i = 0; i < n; i ++) res = max(res, f[i]); //枚举所有的终点
    cout << res << endl;
    return 0;
}

优化后的最长上升子序列代码：（1<=N<=10,0000）$O(NlogN)$
DP + 二分

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 100010;
int n;
int a[N], q[N]; //q[]存所有不同长度的最长上升子序列结尾的最小值
int f[N];

int main (){
    cin >> n;
    for (int i = 0; i < n; i ++) cin >> a[i];
    int len = 0; //长度开始设为0，当前长度的最大长度len，即q[]数组中实际元素的个数，开始是0
    q[0] = -2e9; //为了保证数组当中小于某个数一定是存在的，把q[0]当成哨兵

    for (int i = 0; i < n; i ++) { //枚举每一个数
        int l = 0, r = len;
        while (l < r) { //此处二分出小于某个数的最大的数（边界问题是用q[0] = -2e9解决的）
            int mid = l + r + 1 >> 1;
            if (q[mid] < a[i]) l = mid; //这里是l = mid 则上面一行出 “上取整” 记得 +1 
            else r = mid - 1;
        }
        len = max(len, r + 1); //更新len最大值
        q[r + 1] = a[i]; //做完后，直接把q[len]更新成a[i]
    }

    cout << len << endl;
    return 0;
}

模板1：下取整

int bsearch_1(int l, int r) {
    while (l < r) {
        int mid = l + r >> 1;
        if (check(mid))  r = mid;
        else l = mid + 1；
    }
    return l;
}

模板2：上取整

int bsearch_2(int l, int r) {
    while (l < r) {
        int mid = l + r + 1 >> 1;
        if (check(mid))  l = mid;
        else r = mid - 1；
    }
    return l;
}

怎么输出最长上升子序列的序列呢？$O(N^2)$

这里是逆序（如果要正序输出可以用栈存储或者用reverse()）

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 1010;
int n;
int a[N];
int f[N], g[N];

int main (){
    cin >> n;
    for (int i = 0; i < n; i ++) cin >> a[i];

    for (int i = 0; i < n; i ++) {
        f[i] = 1;
        g[i] = 0;

        for (int j = 0; j < i; j ++) {
            if (a[j] < a[i])
                if (f[i] < f[j] + 1) {
                    f[i] = f[j] + 1;
                    g[i] = j;
                }
        }
    }

    //这里是要找到f[0]~f[n]中的最大值，以及最大值的下标，所以使用if 比较判断，然后更新下标，和优化版前的版本不一样，因为那里不需要求出最大值下标，所以直接用max()
    int k = 1;
    for (int i = 0; i < n; i ++) 
        if (f[k] < f[i])
            k = i;

    cout << f[k] << endl;

    for (int i = 0, len = f[k]; i < len; i ++) { //必须用len临时记录f[k]，因为f[k]的值会随着循环变化（k变化了）
        cout  << a[k] << ' '; //最大值下标的用处就在这里和下一行
        k = g[k];
    }

    return 0;
}