*****1.从上到下走********
状态转移方程
f[i][j] = max(f[i - 1][j] + w[i][j], f[i - 1][j - 1] + w[i][j]);

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 510, INF = 1e9;
int n;
int w[N][N],f[N][N];


int main (){
    cin >> n;
    for (int i = 1; i <= n; i ++)   
        for (int j = 1; j <= i; j ++)
            cin >> w[i][j];

    for (int i = 1; i <= n; i ++)
        for (int j = 0; j <= i + 1; j ++) // 这里易错！！！j<=i+1;不是j<=i 因为要考虑边界问题，j需要枚举到i+1，就是每一行最后要多一个数，因为求每行末尾的f[][]时，需要右上方的值，所以需要设置多一个为-∞
            f[i][j] = -INF;

    f[1][1] = w[1][1]; //容易和上面的for循环颠倒位置，一定是先初始化为-∞，然后确定边界

    for (int i = 2; i <= n; i ++) //这里就可以从2开始了，因为i=1只有一个数
        for (int j = 1; j <= i; j ++)
            f[i][j] = max(f[i - 1][j] + w[i][j], f[i - 1][j - 1] + w[i][j]); //糊涂了，写成f[i][j]=max(f[i+1][j]+w[i][j],f[i+1][j+1]+w[i][j];

    int res = -INF;

    for (int i = 1; i <= n; i ++)
        res = max(res, f[n][i]);

    cout << res << endl;

    return 0;
}

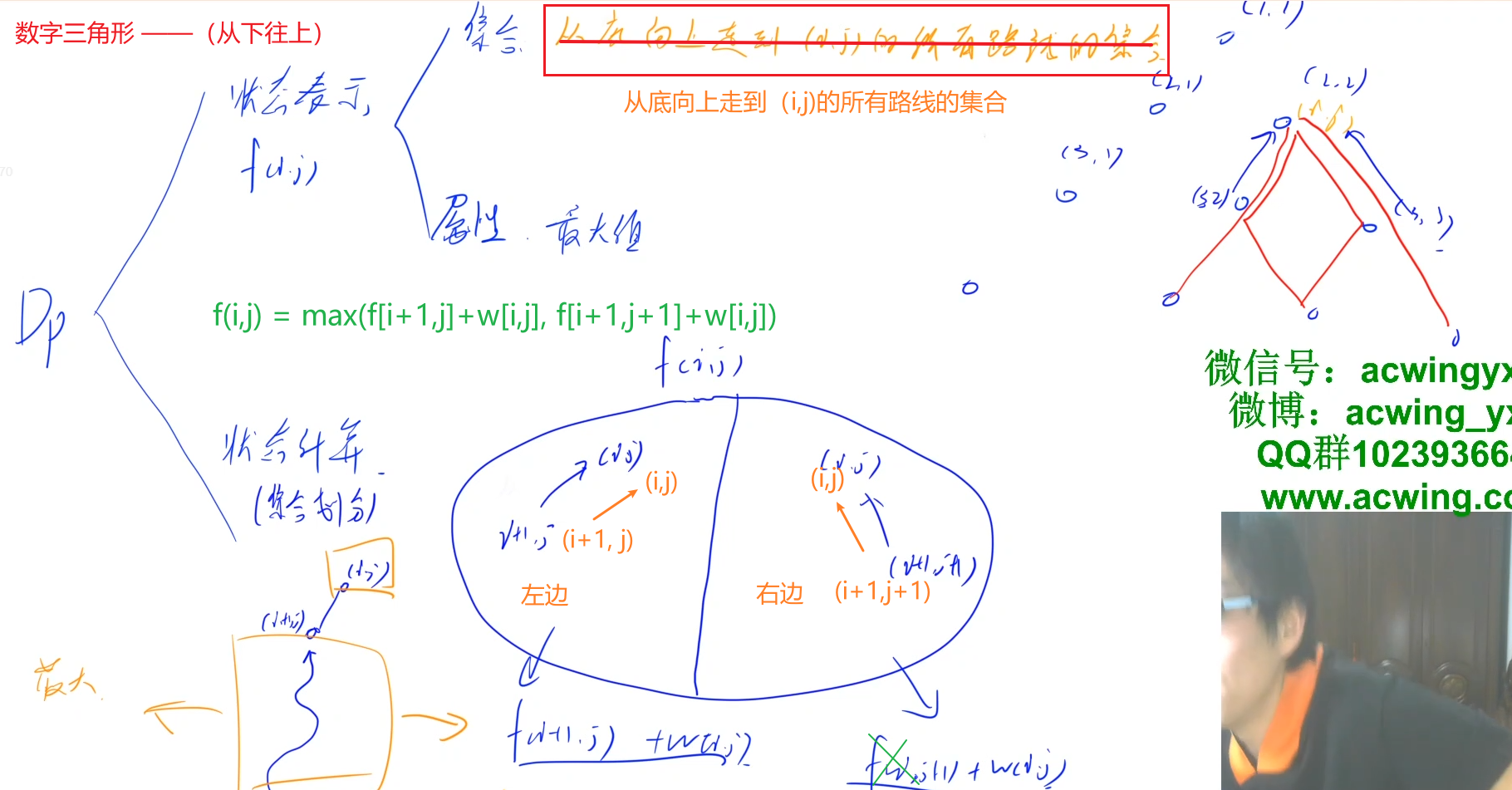
*****2.从下到上走*********
状态转移方程
f[i][j] = max(f[i + 1][j] + w[i][j], f[i + 1][j + 1] + w[i][j]);

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 510, INF = 1e9;
int n;
int w[N][N],f[N][N];

int main () {
    cin >> n;
    for (int i = 1; i <= n; i ++)
        for (int j = 1; j <= i; j ++)
            cin >> w[i][j];

    for (int i = 1; i <= n; i ++) f[n][i] = w[n][i];

    for (int i = n -1; i > 0; i --)
        for (int j = 1; j <= i; j ++)
            f[i][j] = max(f[i + 1][j] + w[i][j], f[i + 1][j + 1] + w[i][j]);

    cout << f[1][1] << endl;
    return 0;
}

*****3.简化2********
状态转移方程
f[i][j] = max(f[i + 1][j], f[i + 1][j + 1]) + f[i][j];

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 510, INF = 1e9;
int n;
int f[N][N];

int main () {
    cin >> n;
    for (int i = 1; i <= n; i ++)
        for (int j = 1; j <= i; j ++)
            cin >> f[i][j];

    for (int i = n -1; i > 0; i --)
        for (int j = 1; j <= i; j ++)
            f[i][j] = max(f[i + 1][j], f[i + 1][j + 1]) + f[i][j];

    cout << f[1][1] << endl;
    return 0;
}

*****4.降维2*******
状态转移方程
f[i & 1][j] = max(f[i + 1 & 1][j], f[i + 1 & 1][j + 1]) + w[i][j];

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 510, INF = 1e9;
int n;
int w[N][N], f[2][N];

int main () {
    cin >> n;
    for (int i = 1; i <= n; i ++)
        for (int j = 1; j <= i; j ++)
            cin >> w[i][j];

    for (int i = 1; i <= n; i ++)   f[n & 1][i] = w[n][i]; //只给f[][]的第一维加 &1，不用给w[n][i]加

    for (int i = n - 1; i > 0; i --)
        for (int j = 1; j <= i; j ++)
            f[i & 1][j] = max(f[i + 1 & 1][j], f[i + 1 & 1][j + 1]) + w[i][j];

    cout << f[1 & 1][1] << endl;
    return 0;
}

3.简化版数字三角形 O(n2)
1. 对于代码 f[i][j] = max( +w[][], +w[][]) 提出共同的w[i][j]
2. 把w[][]和f[][]合二为一 ，将w[][] 换成 f[][]
3. f[i][j] += max( , ) ; 使用 += 运算

4.降维版数字三角形–进行降维–二维降为一维 O(n2)
降维的标准做法：
1. 把 f[N][N] 第一维改成 f[2][N] —> “滚动数组”
2. 把后面所有用到的 f[][] 的第一维加上 &1 即可， “&1” 相当于 模2运算
因为 & 运算符优先级低于 + 所以 f[i + 1 & 1][j] 不用加括弧

最初的题解可能更详细，转到 数字三角形 （包含golang代码）

1和2对应的图

图1

图2