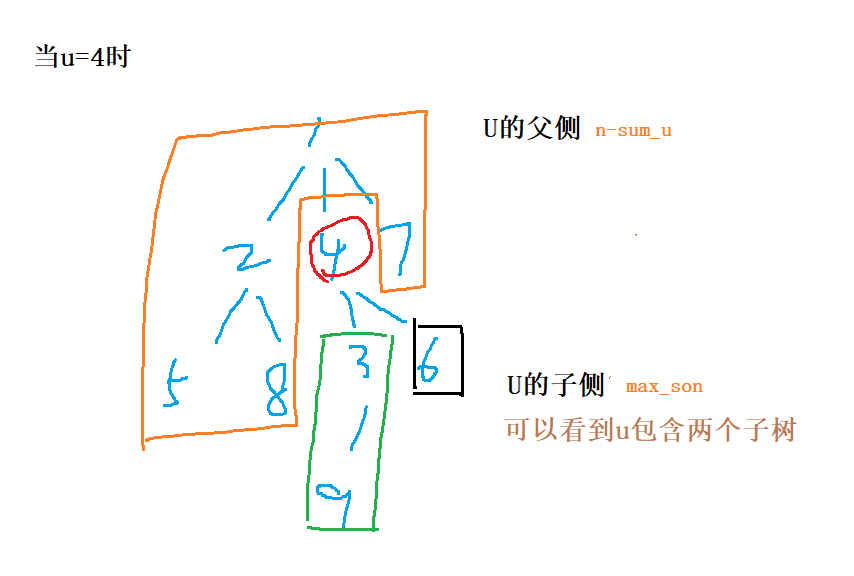
由于我抽象能力实在不行，故画了讨论4号节点时的图，更好理解一些。
要说的话都写到注释中了

#include <iostream>
#include <queue>
#include <cstring>
#include <algorithm>
using namespace std;

const int N = 100010;
int h[N], e[2 * N], ne[2 * N], idx; // 边数最大可达节点数的2倍
int n, v[N], ans = N;

void add(int a, int b) // 将b挂到a链上
{
    e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}

int DFS(int u)
{
    v[u] = 1;
    int max_son = 0; // 删掉u后，会生成若干u的子树，找出其中连通块最大的值
    int sum_u = 1; // 以u为根的子树总节点数（计算父侧节点数要用）
    for (int i = h[u]; i != -1; i = ne[i])
    {
        int j = e[i];
        if (v[j] == 0)
        {
            int t = DFS(j); // 获取到j子树的总结点数（注意此时不包括u）
            max_son = max(max_son, t); // 获得子侧最大连通块值
            sum_u += t; // 遍历完毕u的一颗子树，累加节点数
        }
    }
    ans = min(ans, max(max_son, n - sum_u)); // 先对父侧、子侧求最大连通块值
    return sum_u; // 返回以u为根的子树总节点数
}

int main()
{
    memset(h, -1, sizeof h);
    cin >> n;
    for (int i = 0; i < n - 1; i++)
    {
        int a, b;
        cin >> a >> b;
        add(a, b), add(b, a);
    }
    DFS(1);
    cout << ans << endl;
    return 0;
}