DP + 贪心 双解 （附贪心证明）

一、状态机模型DP解法

我这里直接贴出闫氏DP分析法的思维导图

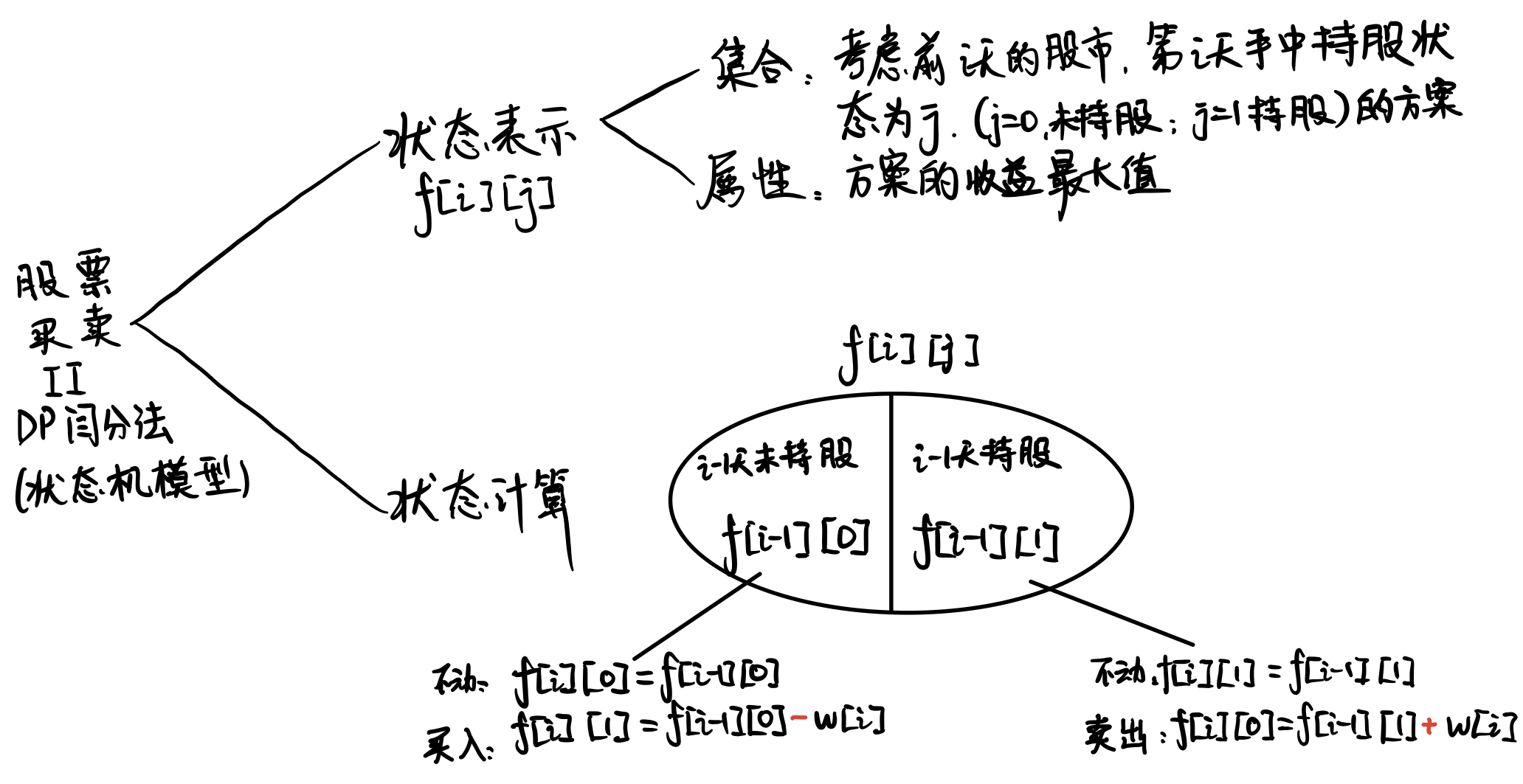
具体的状态机模型分析如下图:

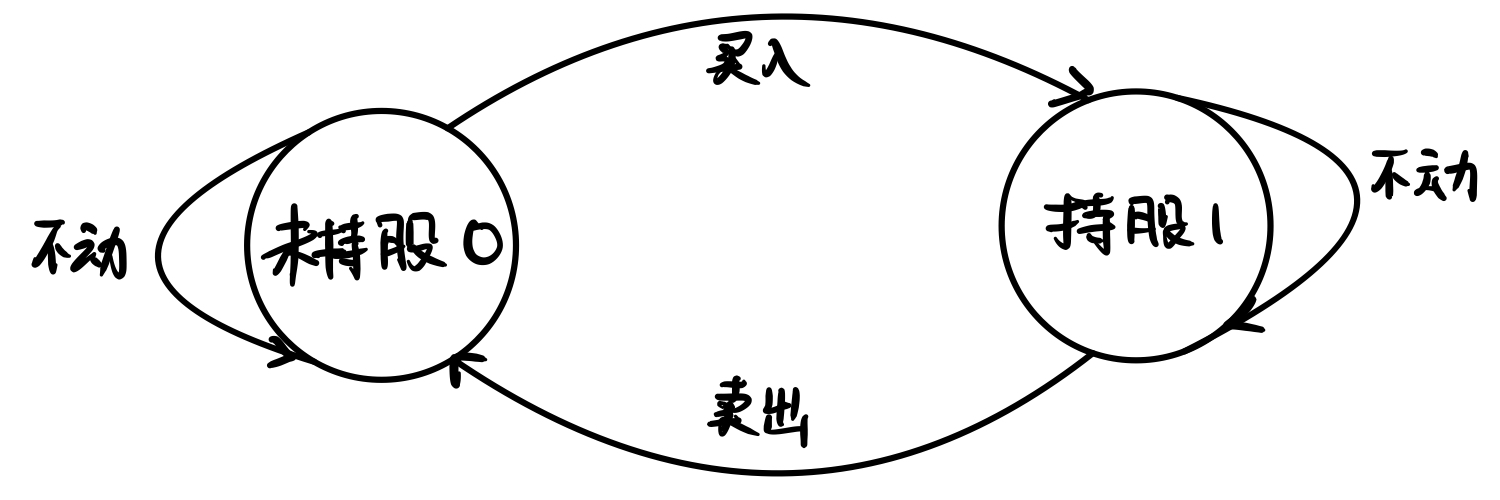
一共只$2$有种状态:

1. 当前处于未持股状态0：

对应可以进行的转换：
    0->0 （不买入，继续观望，那么就什么都不发生）
    0->1 （买入股票，那么收益就要减去当前市场的股票价格）

2. 当前处于持股状态1：

对应可以进行的转换：
    1->1 （不卖出，继续观望，那么就什么都不发生）
    1->0 （卖出股票，那么收益就要加上当前市场的股票价格）

Code:

#include <iostream>
using namespace std;
const int N = 1e5 + 10, INF = 0x3f3f3f3f;
int n;
int w[N];
int f[N][2];

int main() {
    scanf("%d", &n);
    for (int i = 1; i <= n; ++i) scanf("%d", &w[i]);

    f[0][1] = -INF;
    for (int i = 1; i <= n; ++i) {
        f[i][0] = max(f[i - 1][0], f[i - 1][1] + w[i]);
        f[i][1] = max(f[i - 1][1], f[i - 1][0] - w[i]);
    }
    printf("%d\n", f[n][0]);
    return 0;
}

二、贪心解法

纵然，我们可以用DP搜索出所有的方案数，但是通过观察，我们可以发现本题最优解方案存在一定的性质。

我先贴出测试样例的折线图形式（绿色标出下降，红色标出上升）：

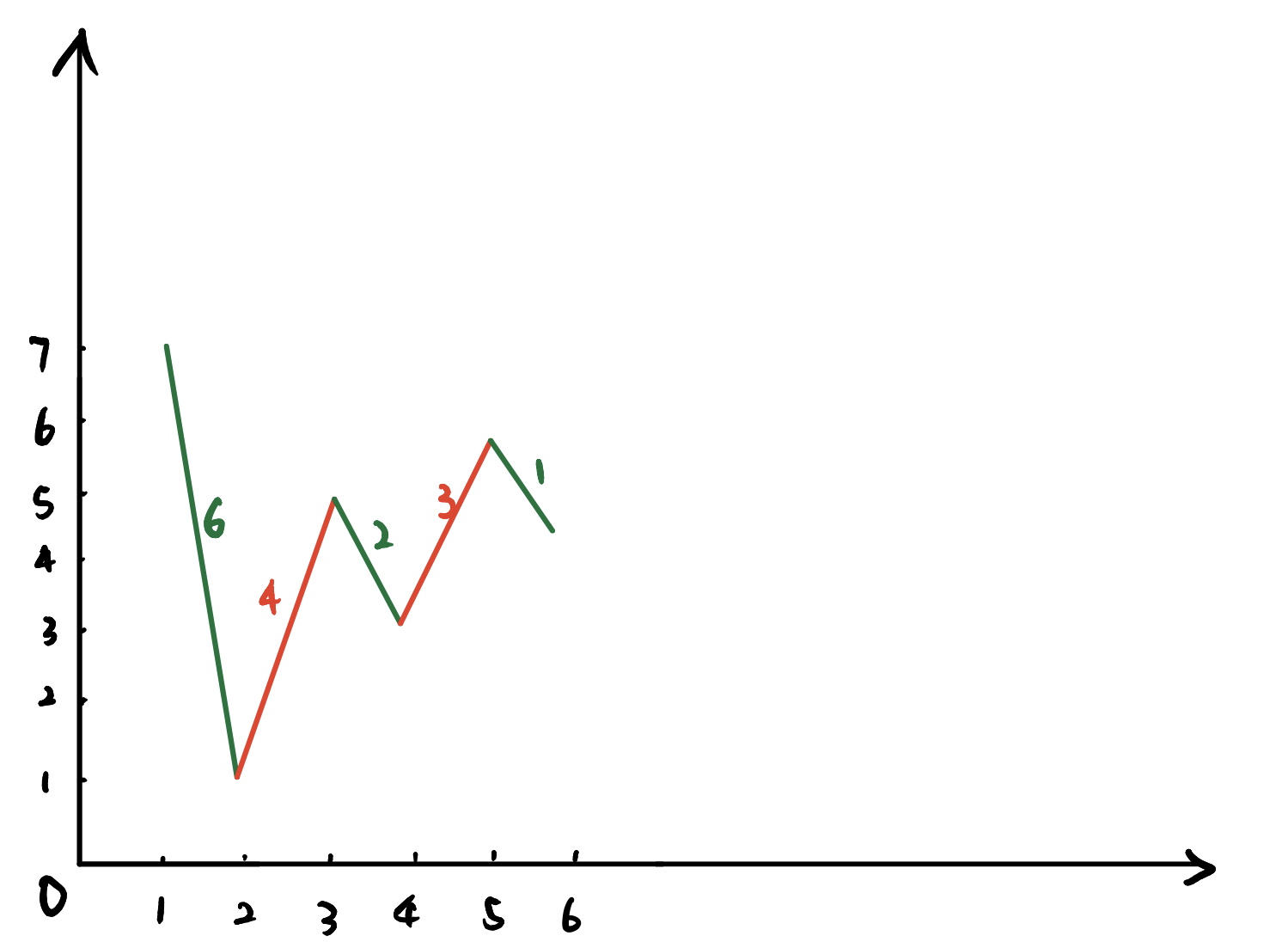
考虑一种方案，在每次上升的前一天购入股票，并在上升后的当天卖出的方案

if (w[i] > w[i - 1])
    res += w[i] - w[i - 1];

接下来证明该贪心思路得出的方案即是最优解。

（1）证明贪心解 $\ge$ 最优解：

由于贪心解都是取区间长度为 $1$ 的解，因此假设存在于最优解中的某个区间 $[i, j]$ 的长度 $ > 1$

那么会出现一下三种情况：

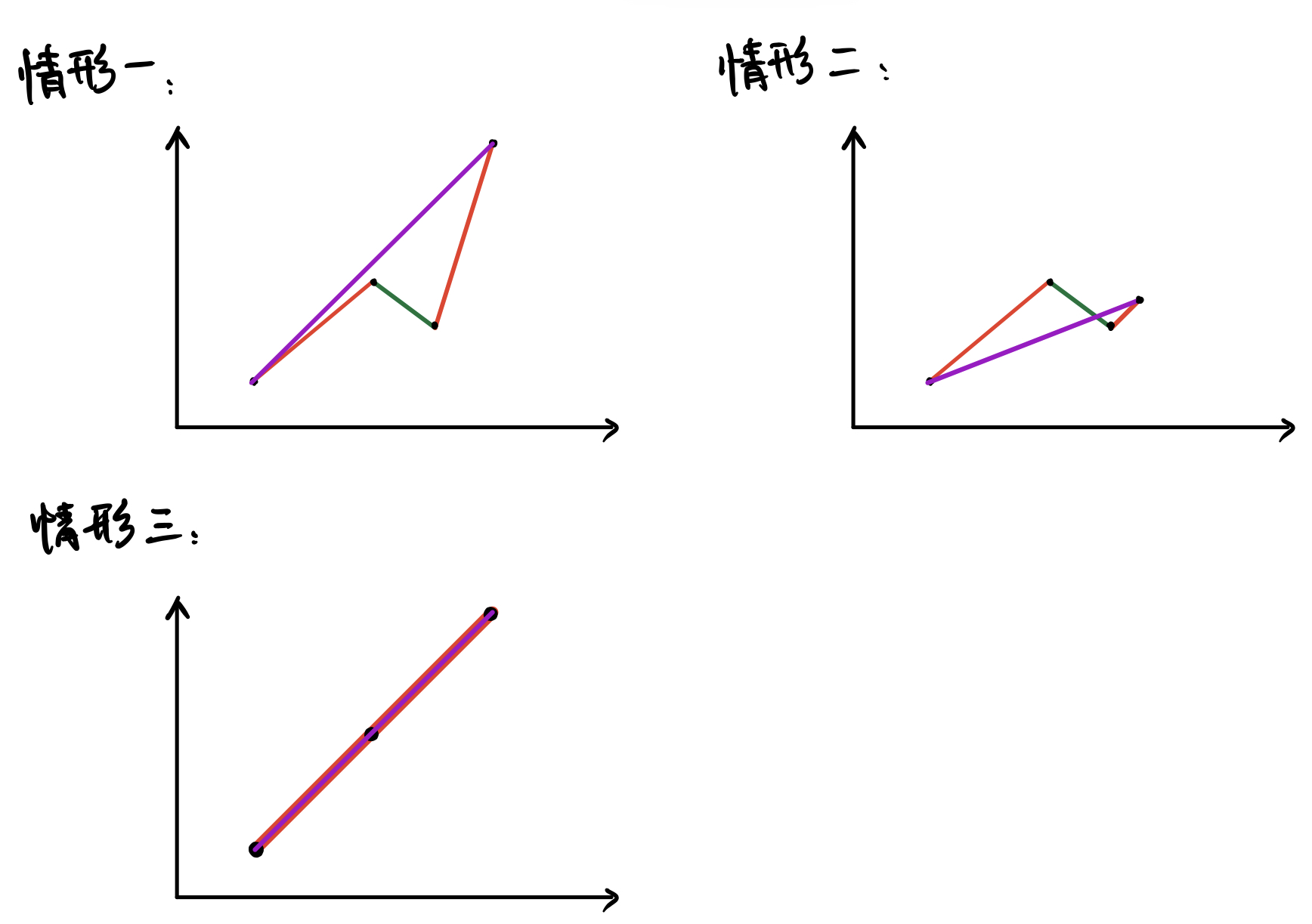
对应三种情形：最优解选取的区间最终点位于上方、下方、相等。

对于情形一：显然 最优解 $ < $ 贪心解
对于情形二：显然 最优解 $ < $ 贪心解
对于情形三：毫无疑问，这就是存在于贪心解中的情形，因此 贪心解 $=$ 最优解

得证

（2）证明贪心解 $\le$ 最优解：

这部分无需证明，因为贪心解即是合法解，所以他的方案必定大于等于最优解

Code

#include <iostream>
using namespace std;
const int N = 1e5 + 10, INF = 0x3f3f3f3f;
int n;
int w[N];

int main() {
    scanf("%d", &n);
    for (int i = 1; i <= n; ++i) scanf("%d", &w[i]);

    int res = 0;
    for (int i = 2; i <= n + 1; ++i) {
        if (w[i] - w[i - 1] > 0) res += w[i] - w[i - 1];
    }
    printf("%d\n", res);
    return 0;
}